题目内容
16.因式分解:(1)16-4x2
(2)9a2(x-y)-4(x-y)
(3)(x2+4)2-16x2.
分析 (1)原式提取公因式,再利用平方差公式分解即可;
(2)原式提取公因式,再利用平方差公式分解即可;
(3)原式利用平方差公式及完全平方公式分解即可.
解答 解:(1)原式=4(4-x2)=4(2+x)(2-x);
(2)原式=(x-y)(9a2-4)=(x-y)(3a+2)(3a-2);
(3)原式=(x2+4+4x)(x2+4-4x)=(x+2)2(x-2)2.
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
4.在平行四边形ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是( )
| A. | 2<AD<18 | B. | 1≤AD≤9 | C. | 2≤AD≤8 | D. | 1<AD<9 |
8.关于x的方程(a-6)x2-8x+6=0有实数根,下列整数不满足a的取值的是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
5.下列式子正确的是( )
| A. | ±$\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | $\sqrt{{(-3)}^{2}}$=-3 | D. | ±$\sqrt{4}$=2 |
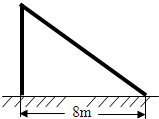 如图所示,台风过后,旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆在离地面6米处折断,请你求出旗杆原来的高度?
如图所示,台风过后,旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆在离地面6米处折断,请你求出旗杆原来的高度?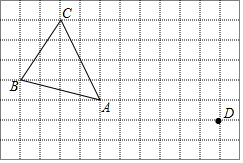 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点. 如图,直线y=x+2与双曲线y=$\frac{k}{x}$相交于点A,点A的纵坐标为3,则k的值为( )
如图,直线y=x+2与双曲线y=$\frac{k}{x}$相交于点A,点A的纵坐标为3,则k的值为( )