题目内容
11. 如图,△ABC内接于⊙O,D是$\widehat{BC}$的中点,点E在AD上,且DE=DB,点E是△ABC的内心吗?并说明理由.
如图,△ABC内接于⊙O,D是$\widehat{BC}$的中点,点E在AD上,且DE=DB,点E是△ABC的内心吗?并说明理由.
分析 根据等弧所对的圆周角相等证明∠BAD=∠CAD,根据等腰三角形的性质和三角形的外角的性质证明∠EBC=∠ABE,根据内心的概念证明结论.
解答 解:点E是△ABC的内心,
证明如下:∵D是$\widehat{BC}$的中点,
∴$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CAD,
∵DE=DB,
∴∠DBE=∠DEB,即∠DBC+∠EBC=∠BAD+∠ABE,
∵$\widehat{BD}$=$\widehat{CD}$,∴∠DBC=∠BAD,
∴∠EBC=∠ABE,又∠BAD=∠CAD,
∴点E是△ABC的内心.
点评 本题考查的是三角形的内切圆和内心的概念和性质,掌握三角形的内心是三角形三条角平分线的交点是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
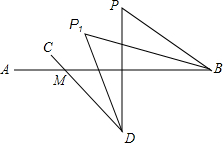 如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
 如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.