题目内容
6.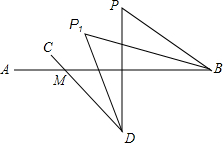 如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
如图,BP1平分∠ABP,DP1平分∠CDP,将直线CD绕点D按顺时针方向旋转一定角度交直线AB于点M,判断∠P,∠P1,∠BMD的数量关系,并证明.
分析 连接BD,根据三角形内角和定理和邻补角的定义即可求得结论.
解答  解:连接BD,
解:连接BD,
∠P1=180°-(∠+∠2)-$\frac{1}{2}$(∠PDC+∠PBA)
=∠BOD-$\frac{1}{2}$(∠PDC+∠PBA)
=∠BOD-$\frac{1}{2}$(180°-∠AOD-∠BMD+180°-∠POB-∠P)
=∠BOD-$\frac{1}{2}$(∠BOD-∠BMD+∠BOD-∠P)
=$\frac{1}{2}$(∠BMD+∠P).
点评 本题考查了三角形内角和定理和邻补角的概念,熟练掌握内角和定理,找出角之间的关系是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.下列命题中,假命题是( )
| A. | 三角形任意两边中点连接线段与第三边的比等于$\frac{1}{2}$ | |
| B. | 正方形的对角线与一边的比等于$\sqrt{2}$ | |
| C. | 直角三角形的斜边与这边上的中线的比等于2 | |
| D. | 如果一个三角形三个内角的比是1:2:3,那么对应边的比也是1:2:3 |
15. 如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )
如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )
 如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )
如图,在一个腰长为10的等腰直角三角形的内部作一个矩形ABCD,其中B,D分别在边AF,AE上,则此矩形的最大面积为( )| A. | 25 | B. | 24 | C. | 20 | D. | 18 |
 在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).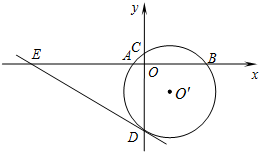 如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$.
如图,已知⊙O′与x轴交于A、B两点,与y轴交于C、D两点,圆心O′的坐标是(1,-1),半径为$\sqrt{5}$. 如图,△ABC内接于⊙O,D是$\widehat{BC}$的中点,点E在AD上,且DE=DB,点E是△ABC的内心吗?并说明理由.
如图,△ABC内接于⊙O,D是$\widehat{BC}$的中点,点E在AD上,且DE=DB,点E是△ABC的内心吗?并说明理由.
