Question

3．如图用同样规格的正方形瓷砖铺设矩形地面，请观察下列图形并解答问题；
（1）在第n个图形中每一横行共有n+2块瓷砖，每一竖行共有n+1块瓷砖；（均用含n的代数式表示）
（2）按上述铺设方案，铺一块这样的矩形地面共用了420块瓷砖，求此时每一横行用了多少块瓷砖？

Answer 1

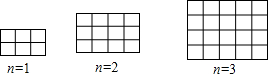
分析 （1）由图分析可知后面图形是在原有基础上个加一行一列，第一个图形2行3列，第二个图形3行4列，…在第n个图形中每一横行共有n+2块瓷砖，每一竖行共有n+1块瓷砖；
（2）第一个图形2行3列，砖块数位2×3=6，第二个图形3行4列，砖块数位3×4=12，…第n个有（n+2）×（n+1），列出方程求解即可．

解答 解：（1）由图形我们不难看出在第n个图形中每一横行共有n+2块瓷砖，每一竖行共有n+1块瓷砖；
（2）由题意可知：
（n+2）×（n+1）=420
解得：n=19
19+2=21
答：此时每一横行用了21块瓷砖．

点评 此题考查书图形的变化规律，找出图形之间的联系，得出运算规律，利用规律解决问题．