题目内容
1.已知a-$\frac{1}{a}$=-$\sqrt{5}$,求$\sqrt{a}$-$\frac{1}{\sqrt{a}}$.分析 先把已知条件两边平方得到(a-$\frac{1}{a}$)2=5,再利用完全平方公式变形得到(a+$\frac{1}{a}$)2=9,则a+$\frac{1}{a}$=3(a>0),则可计算出($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2=a-2+$\frac{1}{a}$=1,然后根据算术平方根的定义求解.
解答 解:∵a-$\frac{1}{a}$=-$\sqrt{5}$,
∴(a-$\frac{1}{a}$)2=5,
∴(a+$\frac{1}{a}$)2-4=5,
∴(a+$\frac{1}{a}$)2=9,
∴a+$\frac{1}{a}$=3或a+$\frac{1}{a}$=-3(因为a>0,故舍去)
∴($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2=a-2+$\frac{1}{a}$=3-2=1,
∴$\sqrt{a}$-$\frac{1}{\sqrt{a}}$=1.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
16.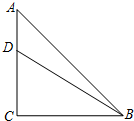 如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
 如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )
如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA=$\frac{1}{5}$,则tan∠CBD的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
10.将1、2、3三个数字分别作为横坐标和纵坐标,随机生成的点的坐标如下表.如果每个点出现的可能性相等,那么从中任意取一点,则这个点的函数y=x图象上的概率是$\frac{1}{3}$.
| (1,1) | (1,2) | (1,3) |
| (2,1) | (2,2) | (2,3) |
| (3,1) | (3,2) | (3,3) |
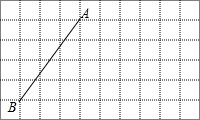 如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.
如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.