题目内容
9.当x=$\frac{1}{2}$,y=-$\frac{1}{3}$时,求代数式2x(x+2y)2-(2y+x)2(x-2y)的值.分析 先根据完全平方公式算乘法,再根据多项式乘以单项式或多项式乘以多项式进行计算,合并同类项,最后代入求出即可.
解答 解:2x(x+2y)2-(2y+x)2(x-2y)
=2x(x2+4xy+4y2)-(4y2+4xy+x2)(x-2y)
=2x3+8x2y+8xy2-4xy2+8y3-4x2y+8xy2-x3+2x2y
=x3+6x2y+12xy2+8y3,
当x=$\frac{1}{2}$,y=-$\frac{1}{3}$时,原式=($\frac{1}{2}$)3+6×($\frac{1}{2}$)2×(-$\frac{1}{3}$)+12×$\frac{1}{2}$×(-$\frac{1}{3}$)2+8×(-$\frac{1}{3}$)3=$\frac{1}{216}$.
点评 本题考查了整式的混合运算和求值的应用,能根据整式的运算法则进行化简是解此题的关键,此题是一道中档题目,难度适中.

练习册系列答案
相关题目
4.二元一次方程组$\left\{\begin{array}{l}{2x-y=2}\\{x+y=4}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ |
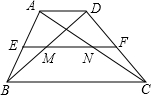 如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.
如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.