题目内容
13.用配方法解下列方程:(1)x2-4x+3=0;
(2)2x2+3=7x;
(3)3x2+4x-7=0;
(4)(x-3)2-4(x-3)-45=0.
分析 根据配方法的步骤先把常数项移到等号的右边,再把二次项的系数化为1,然后在左右两边同时加上一次项系数的一半的平方,配成完全平方的形式,最后开方即可.
解答 解:(1)x2-4x+3=0,
x2-4x=-3,
x2-4x+4=1,
(x-2)2=1,
x-2=±1,
x1=3,x2=1;
(2)2x2+3=7x,
2x2-7x+3=0,
x2-$\frac{7}{2}$x=-$\frac{3}{2}$,
x2-$\frac{7}{2}$x+$\frac{49}{16}$=-$\frac{3}{2}$+$\frac{49}{16}$,
(x-$\frac{7}{4}$)2=$\frac{25}{16}$,
x-$\frac{7}{4}$=±$\frac{5}{4}$,
x1=3,x2=$\frac{1}{2}$;
(3)3x2+4x-7=0,
3x2+4x=7,
x2+$\frac{4}{3}$x=$\frac{7}{3}$,
x2+$\frac{4}{3}$x+$\frac{4}{9}$=$\frac{7}{3}$+$\frac{4}{9}$,
(x+$\frac{2}{3}$)2=$\frac{25}{9}$,
x+$\frac{2}{3}$=±$\frac{5}{3}$,
x1=1,x2=-$\frac{7}{3}$;
(4)(x-3)2-4(x-3)-45=0,
(x-3)2-4(x-3)=45,
(x-3)2-4(x-3)+4=49,
[(x-3)-2]2=49,
x-5=±7,
x1=12,x2=-2.
点评 此题考查了配方法解一元二次方程,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ |
| A. | a>5 | B. | a≥1 | C. | a<5 | D. | a>1 |
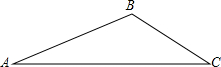 如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,
如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,