题目内容
12.已知:|a-2|+b2-2b+1=0,则ba=1.分析 利用配方法得到|a-2|+(b-1)2=0,利用非负数的性质易得a=2,b=1,然后乘方的意义计算即可.
解答 解:∵:|a-2|+b2-2b+1=0,
∴|a-2|+(b-1)2=0,
∴a-2=0,b-1=0,解得a=2,b=1,
∴ba=12=1.
故答案为1.
点评 本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
相关题目
4.二元一次方程组$\left\{\begin{array}{l}{2x-y=2}\\{x+y=4}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ |
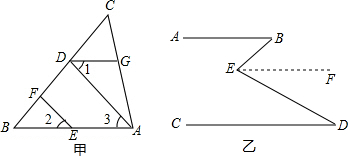 仔细想一想,完成下面的推理过程.
仔细想一想,完成下面的推理过程.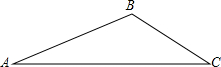 如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,
如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,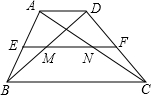 如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.
如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.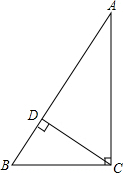 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.