题目内容
15.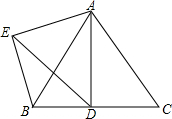 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.(1)求证:△ADE是等边三角形;
(2)当点D在何处时,AE⊥BE?指出点D的位置并说明理由.
分析 (1)根据等边三角形的性质得到AB=AC,∠BAC=∠C=60°,由∠DAE=60°得到∠DAE=∠BAC,推出∠EAB=∠DAC,根据平行线的性质得到∠EBA=∠BAC,推出∠EBA=∠C,证得△AEB≌△ADC,根据全等三角形的性质得到AE=AD,即可得到结论;
(2)当D为AC中点时.根据等腰三角形的性质得到AD⊥BC,于是得到∠ADC=90°,根据全等三角形的性质得到∠AEB=∠ADC=90°,于是得到结论.
解答 证明:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
∵∠DAE=60°
∴∠DAE=∠BAC,
∴∠DAE-∠BAD=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∵BE∥AC,
∴∠EBA=∠BAC,
∴∠EBA=∠C,
在△AEB和△ADC中,
$\left\{\begin{array}{l}{∠EAB=∠DAC}\\{AB=AC}\\{∠EBA=∠C}\end{array}\right.$,
∴△AEB≌△ADC,
∴AE=AD,
∵∠DAE=60°,
∴△ADE是等边三角形;
(2)当D为AC中点时.
∵AB=AC,D为AC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵△AEB≌△ADC,
∴∠AEB=∠ADC=90°,
∴AE⊥BE.
点评 本题考查了全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的性质,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.
将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.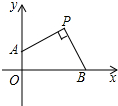 如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.
如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.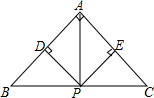 在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:
在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证: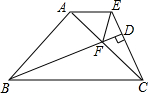 如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.
如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.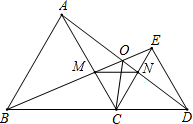 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( )
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( ) 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.