题目内容
5.(1)解方程:$\frac{x}{x-2}+\frac{2}{{{x^2}-4}}=1$(2)解不等式:1-$\frac{3x+1}{5}$≤$\frac{x-1}{2}$-2.
分析 (1)观察方程可得最简公分母是(x-2)(x+2),两边同时乘最简公分母可把分式方程化为整式方程来解答;
(2)根据一元一次不等式的解法先去分母、去括号,再移项、合并同类项、系数化为1,即可求得不等式的解集.
解答 解:(1)方程两边同乘(x-2)(x+2),
得x(x+2)+2=(x-2)(x+2),
解得,x=-3.
检验:把x=-3代入(x-2)(x+2)=5≠0,
所以原方程的解为x=-3;
(2)去分母得,10-2(3x+1)≤5(x-1)-20,
去括号得,10-6x-2≤5x-5-20,
移项合并得,11x≥33,
系数化为1得,x≥3.
点评 本题考查的是解分式方程与解一元一次不等式.解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解;解分式方程一定注意要验根.解不等式要依据不等式的基本性质:不等式的两边同时加上或减去同一个数或整式不等号的方向不变;不等式的两边同时乘以或除以同一个正数不等号的方向不变;不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
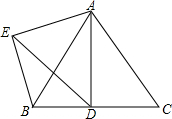 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.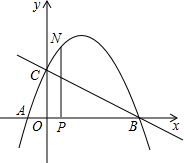 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC. 表示运算x+z-y-w.则
表示运算x+z-y-w.则 =-2.
=-2. 已知:如图,线段a.求作:正方形ABCD,使正方形ABCD的对角线AC=a.
已知:如图,线段a.求作:正方形ABCD,使正方形ABCD的对角线AC=a.