题目内容
7. 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
分析 根据正方形性质求出AD=AB,∠DAE=90°,求出∠BFE=∠DAE=∠FAG=90°,∠FAB=∠DAG,根据∠ADG=180°-∠DAG-∠AED,∠ABF=180°-∠BFE-∠BEF求出∠ADG=∠ABF,根据ASA推出△DAG≌△BAF,根据全等三角形的性质得出AF=AG,求出∠AFG=∠AGF=45°,即可得出答案.
解答 证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=90°,
∵AF⊥AG,BF⊥DE,
∴∠BFE=∠DAE=∠FAG=90°,
∴∠FAB=∠DAG=90°-∠GAE,
∵∠ADG=180°-∠DAG-∠AED,∠ABF=180°-∠BFE-∠BEF,
又∵∠DAE=∠BFE,∠AED=∠BEF,
∴∠ADG=∠ABF,
在△DAG和△BAF中,
$\left\{\begin{array}{l}{∠ADG=∠ABF}\\{AD=AB}\\{∠DAG=∠BAF}\end{array}\right.$,
∴△DAG≌△BAF(ASA),
∴AF=AG,
∵∠FAG=90°,
∴∠AFG=∠AGF=45°,
∴∠AGD=∠GAF+∠AFG=90°+45°=135°.
点评 本题考查了正方形性质,全等三角形的性质和判定,三角形内角和定理,三角形外角性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
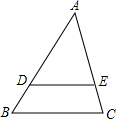 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.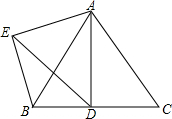 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.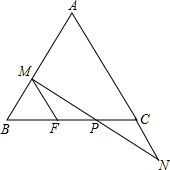 在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.
在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN. 如图,将矩形纸片ABCD沿AE折叠,点B恰好落在AC上的点F处,若AB=1,BC=2,求BE的长.
如图,将矩形纸片ABCD沿AE折叠,点B恰好落在AC上的点F处,若AB=1,BC=2,求BE的长.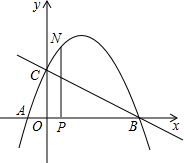 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.