题目内容
10.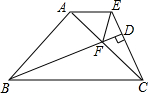 如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.
如图,△ABC中,∠BAC=90°,AB=AC,AE∥BC,BD⊥CE于点D,BD交AC于F,连结EF.求证:BF=CE+EF.
分析 延长BA,CE交于E,根据等腰直角三角形的性质得到∠ACB=45°,∠HAF=90°,根据平行线的性质得到∠EAF=∠ACB=∠ABC=∠EAH=45°,根据预计欧的性质得到∠1=∠4,推出△ABF≌△ACH,由全等三角形的性质得到BF=CH,AF=AH,通过△AEF≌△AEH,得到EF=HE,于是得到结论.
解答 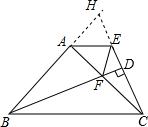 证明:延长BA,CE交于E,
证明:延长BA,CE交于E,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,∠HAF=90°,
∵AE∥BC,
∴∠EAF=∠ACB=∠ABC=∠EAH=45°,
∵∠1+∠2=∠3+∠4=90°,∠2=∠3,
∴∠1=∠4,
在△ABF与△ACH中,$\left\{\begin{array}{l}{∠BAF=∠CAH}\\{AB=AC}\\{∠1=∠4}\end{array}\right.$,
∴△ABF≌△ACH,
∴BF=CH,AF=AH,
在△AEF与△AEH中,$\left\{\begin{array}{l}{AH=AF}\\{∠HAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△AEF≌△AEH,
∴EF=HE,
∴BF=CH=CE+HE=CE+EF.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
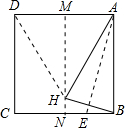 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )
如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )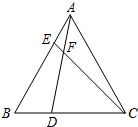 在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F. 已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.
已知:如图,AB∥DC,AB=DC,O是DB上一点,过点O的直线分别交DA和BC的延长线于点E、F.求证:∠E=∠F.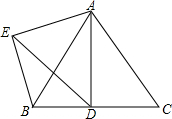 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.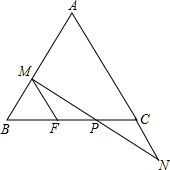 在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.
在△ABC中,AB=AC,P是BC边上的一点,过P引直线分别交AB于M,交AC的延长线于N,且PM=PN,MF∥AN.