题目内容
14.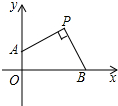 如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.
如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.
分析 过P作PM⊥y轴于M,PN⊥x轴于N,得出四边形PMON是正方形,推出OM=OM=ON=PN=2,证△APM≌△BPN,推出AM=BN,求出OA+OB=ON+OM,代入求出即可.
解答  解:过P作PM⊥y轴于M,PN⊥x轴于N,
解:过P作PM⊥y轴于M,PN⊥x轴于N,
∵P(2,2),
∴PN=PM=2,
∵x轴⊥y轴,
∴∠MON=∠PNO=∠PMO=90°,
∴∠MPN=360°-90°-90°-90°=90°,
则四边形MONP是正方形,
∴OM=ON=PN=PM=2,
∵∠APB=90°,
∴∠APB=∠MON,
∴∠MPA=90°-∠APN,∠BPN=90°-∠APN,
∴∠APM=∠BPN,
在△APM和△BPN中
$\left\{\begin{array}{l}{∠APM=∠BPN}\\{PM=PN}\\{∠PMA=∠PNB}\end{array}\right.$
∴△APM≌△BPN(ASA),
∴AM=BN,
∴OA+OB
=OA+0N+BN
=OA+ON+AM
=ON+OM
=2+2
=4,
故答案为:4.
点评 本题考查了全等三角形的性质和判定,三角形的内角和定理,坐标与图形性质,正方形的性质的应用,关键是推出AM=BN和推出OA+OB=OM+ON.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
2.下列各式中运算正确的是( )
| A. | 3m+2=5m | B. | 2x2-x2=2 | C. | ab-ab=0 | D. | y+y+y=y3 |
 如图所示,画出下列几何体的三种视图.
如图所示,画出下列几何体的三种视图.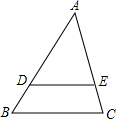 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.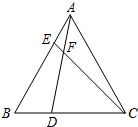 在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.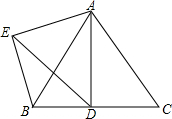 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.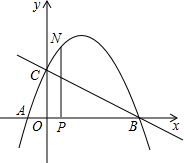 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0),点B(2,0),与y轴交于点C(0,1),连接BC.