题目内容
8.(1)($\sqrt{3}$)2+4×(-$\frac{1}{2}$)-23;(2)$\sqrt{2}$×$\frac{1}{3}$$\sqrt{3}$×$\sqrt{6}$;
(3)$\sqrt{1\frac{3}{5}}$×2$\sqrt{3}$×(-$\frac{1}{2}$$\sqrt{10}$);
(4)(-3)0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$.
分析 (1)根据二次根式的性质和乘方的意义计算;
(2)利用二次根式的乘法法则运算;
(3)利用二次根式的乘法法则运算;
(4)先利用零指数幂的意义计算,再去绝对值和分母有理化,然后合并即可.
解答 解:(1)原式=3-2-8
=-7;
(2)原式=$\frac{1}{3}$$\sqrt{2×3×6}$
=2;
(3)原式=2×(-$\frac{1}{2}$)×$\sqrt{\frac{8}{5}×3×10}$
=-4$\sqrt{3}$;
(4)原式=1-3$\sqrt{3}$+$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$
=-2$\sqrt{3}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
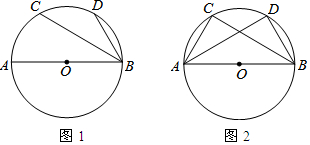
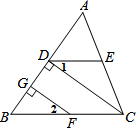 如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2.
如图,已知FG⊥AB,CD⊥AB,垂足分别为G、D,∠1=∠2.