题目内容
18.如图,AB是⊙O的直径,C,D是$\widehat{AB}$上两点,AB=5.(1)如图(1),若点C,D是$\widehat{AD}$的三等分点,求BC的长;
(2)如图(2),若点C是$\widehat{AD}$的中点,BD=3,求BC的长.
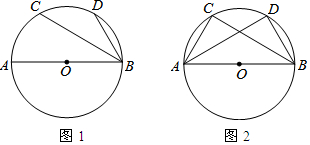
分析 (1)如图1,连接AC,由已知条件得到∠ABC=30°,根据直角三角形的性质即可得到结论;
(2)连接OC,由点C是$\widehat{AD}$的中点,得到OC⊥AD,AH=DH,根据圆周角定理得到∠D=∠ACB=90°,由勾股定理即可得到结论.
解答 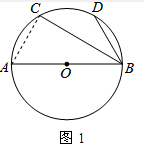 解:(1)如图1,连接AC,
解:(1)如图1,连接AC,
∵点C,D是$\widehat{AD}$的三等分点,
∴$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,
∴∠ABC=30°,
∵AB=5,
∴BC=$\frac{\sqrt{3}}{2}$AB=$\frac{5\sqrt{3}}{2}$;
(2)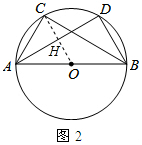 连接OC,
连接OC,
∵点C是$\widehat{AD}$的中点,
∴OC⊥AD,AH=DH,
∵AB是⊙O的直径,
∴∠D=∠ACB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4,
∴AH=2,
∵OH=$\frac{1}{2}$BD=$\frac{3}{2}$,
∴CH=2.5,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\frac{\sqrt{41}}{2}$,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\frac{\sqrt{59}}{2}$.
点评 本题考查了圆周角定理,垂径定理,直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
18.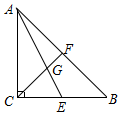 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
 如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )
如图,等腰直角△ABC的中线AE,CF相交于点G,若斜边AB的长为6,则AG长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
6.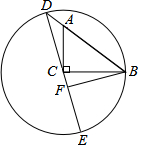 如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
 如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )
如图,直角△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心BC为半径画圆交BA延长线于点D,连接DC并延长交圆C于点E,过点B作DE的垂线BF,垂足为点F,那么线段BF的长度为( )| A. | $\frac{18}{5}$ | B. | 3.5 | C. | $\frac{19}{5}$ | D. | $\frac{96}{25}$ |
 如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.
如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.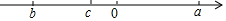 有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.