题目内容
18．已知$\root{3}{x}$=4，且（y-2z+1）2与$\sqrt{z-3}$互为相反数，求$\root{3}{{x+{y^3}+{z^3}}}$的值．分析 利用立方根定义，相反数性质，以及非负数的性质求出x，y，z的值，代入原式计算即可得到结果．
解答 解：根据题意得：x=64，（y-2z+1）2+$\sqrt{z-3}$=0，
解得：x=64，y=5，z=3，
则原式=$\root{3}{64+125+27}$=$\root{3}{216}$=6．
点评 此题考查了实数的运算，相反数，以及非负数的性质，熟练掌握各自的性质是解本题的关键．
练习册系列答案
相关题目
3．某校对八年级的300名学生数学考试作一次调查，在某范围内的得分情况（每个范围含前一个数据，不含后一个数据）如表，则在75分以下这一分数线中的人数为（ ）
| 得分/分 | 60分以下 | 60～75 | 75～90 | 90～100 |
| 频率 | 20% | 25% | 30% | 25% |
| A． | 75人 | B． | 125人 | C． | 135人 | D． | 165人 |
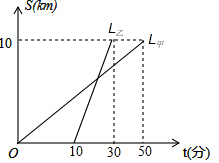甲骑自行车，乙乘公交车，从同一地点出发沿相同路线前往某校参加绘画比赛，图中l甲、l乙分别表示甲、乙两人前往目的地所行使的路程s（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶0.3千米．