题目内容
13.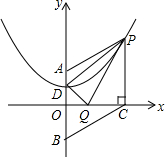 如图,抛物线y=$\frac{1}{4}$x2+bx+c的对称轴是y轴,点D,P在抛物线上,A(0,2),D(0,1),PC⊥x轴于点C,CB∥AP,交x轴于点B.
如图,抛物线y=$\frac{1}{4}$x2+bx+c的对称轴是y轴,点D,P在抛物线上,A(0,2),D(0,1),PC⊥x轴于点C,CB∥AP,交x轴于点B.(1)求抛物线的解析式;
(2)若点P是抛物线上的动点,四边形ABCP是什么特殊的四边形?证明你的结论;
(3)设点Q是x轴上一动点,当(2)中的四边形ABCP是正方形时,△DQP周长是否存在最小值,若存在,请直接写出△DQP周长最小时点Q的坐标;若不存在,请说明理由.
分析 (1)由抛物线的对称轴方程可求得b的值,然后把D(0,1)代入y=$\frac{1}{4}$x2+c可求得c的值,从而可求得抛物线的解析式;
(2)先依据两组对边分别平行的四边形是平行四边形证明四边形ABCP是平行四边形,设点P的坐标是(m,$\frac{1}{4}$m2+1),则PC=$\frac{1}{4}$m2+1.然后依据两点间的距离公式可求得PA的长,从而得到PC=PA,故此可判断出四边形ABCP的形状;
(3)作点D关于x轴的对称点D′.连接PD′交x轴与点Q.由四边形APCB为正方形可知PA∥x轴,点B与点O重合.于是可求得点P的坐标,然后求得直线D′P的解析式,从而可求得点Q的坐标,最后由抛物线的对称性可求得点Q′的坐标.
解答 解:(1)∵抛物线的对称轴是y轴,
∴b=0.
把D(0,1)代入y=$\frac{1}{4}$x2+c得c=1.
∴抛物线的解析式为y=$\frac{1}{4}{x}^{2}$+1.
(2)四边形ABCP是菱形.
∵PC⊥x轴,AB⊥x轴,
∴PC∥AB.
又∵CB∥AP,
∴四边形ABCP是平行四边形.
设点P的坐标是(m,$\frac{1}{4}$m2+1),则PC=$\frac{1}{4}$m2+1.
过点P作PE⊥y轴于点E,则
∴PA2=PE2+AE2=|m|2+|($\frac{1}{4}$m2+1)-2|2=$\frac{1}{16}$m4+$\frac{1}{2}$m2+1=($\frac{1}{4}$m2+1)2.
∴PA=$\frac{1}{4}$m2+1.
∴PC=PA.
∴平行四边形ABCP是菱形.
(3)如图所示:作点D关于x轴的对称点D′.连接PD′交x轴与点Q.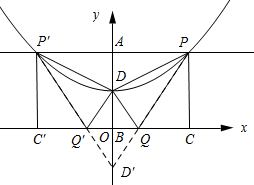
∵四边形APCB为正方形,
∴∠APC=∠PCB=90°.
∴点PA∥x轴,点B与点O重合.
∴点P的纵坐标为2.
将y=2代入y=$\frac{1}{4}{x}^{2}$+1得:$\frac{1}{4}{x}^{2}$+1=2,
解得:x=±2.
∴点P(2,2)、P′(-2,2).
∵点D′与点D关于x轴对称,
∴DQ=D′Q,D′(-1,0).
∴当点D′、Q、P在一条直线上时,PQ+QD有最小值.
又∵DP的长度不变,
∴当点D′、Q、P在一条直线上时,△PDQ的周长最小.
设直线PD′的解析式为y=kx+b.
∵将点P、D′的坐标代入得$\left\{\begin{array}{l}{b=-1}\\{2k+b=2}\end{array}\right.$,解得:k=$\frac{3}{2}$,b=-1,
∴直线PD′的解析式为y=$\frac{3}{2}$x-1.
将y=0代入得;$\frac{3}{2}$x-1=0,解得:x=$\frac{2}{3}$,
∴点Q的坐标为($\frac{2}{3}$,0).
∵点Q′关于点Q对称,
∴Q′(-$\frac{2}{3}$,0).
综上所述,点Q的坐标为($\frac{2}{3}$,0)或Q′(-$\frac{2}{3}$,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、轴对称路径最短问题、平行四边形的判定、菱形的判定,明确当点D′、Q、P在一条直线上时,△PDQ的周长最小时解题的关键.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
| A. |  | B. |  | C. |  | D. |  |
| A. | AD是BC边上的中线 | B. | △ABD≌△ACD | ||
| C. | △ABC是等边三角形 | D. | AB=AC |
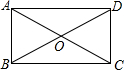 如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可)
如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可)