题目内容
5．方程|x2-4x+3|-k=0有三个实数根，则k的值为（ ）| A． | -2 | B． | 2 | C． | 1 | D． | -1 |
分析 把问题转化为函数y=|x2-4x+3|与直线y=k有3个交点，画出图象即可解决问题．
解答 解：∵方程|x2-4x+3|-k=0有三个实数根，
∴可以看成函数y=|x2-4x+3|与直线y=k有3个交点即可．
函数y=|x2-4x+3|的图象如图所示，
∵y′=x2-4x+3的顶点D坐标为（2，-1），D关于x轴对称点的坐标D′（2，1），
由图象可知，k=1时，函数y=|x2-4x+3|与直线y=k有3个交点，
∴k=1．
故选C．
点评 本题考查二次函数与x轴交点问题，解题的关键是画出函数y=|x2-4x+3|的图象，利用图象法解决问题，属于中考常考题型．
练习册系列答案
相关题目
15．实数-3的绝对值是（ ）
| A． | 3 | B． | -3 | C． | 0 | D． | ±$\sqrt{3}$ |
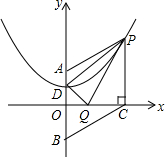如图，抛物线y=$\frac{1}{4}$x2+bx+c的对称轴是y轴，点D，P在抛物线上，A（0，2），D（0，1），PC⊥x轴于点C，CB∥AP，交x轴于点B．
20．下列二次根式中与$\sqrt{3}$是同类二次根式是（ ）
| A． | $\sqrt{18}$ | B． | $\sqrt{30}$ | C． | $\sqrt{48}$ | D． | $\sqrt{54}$ |
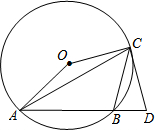如图：△ABC是⊙O的内接三角形，∠ACB=45°，∠AOC=150°，过点C作⊙O的切线交AB的延长线于点D．
画图并回答问题．