题目内容
18.若|x+5y-6|+(3x-6y-4)2=0,则(x-y)2=4.分析 根据非负数的意义得到得$\left\{\begin{array}{l}{x+5y-6=0}\\{3x-6y-4=0}\end{array}\right.$,然后解方程组得到$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,再计算(x-y)2的值.
解答 解:根据题意得$\left\{\begin{array}{l}{x+5y-6=0}\\{3x-6y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,
所以(x-y)2=($\frac{8}{3}$-$\frac{2}{3}$)2=4.
故答案为4.
点评 本题考查了解二元一次方程组:利用加减消元法和代入法解二元一次方程组.也考查了非负数的性质.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
7.在下列各轴对称图案中,对称轴条数相同的是( )


| A. | (1)和(3) | B. | (2)和(4) | C. | (1)、(2)和(3) | D. | (1)、(2)和(4) |
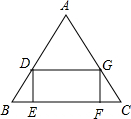 如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;
如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;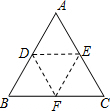 如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.
如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.