题目内容
6.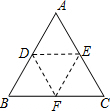 如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.
如图,折叠一张等边三角形纸片ABC,使点A落在BC边上的点,且折痕DE∥BC,问:△DBF和△EFC是不是等边三角形?请说明理由.
分析 首先由等边三角形的性质可知∠B=∠C=60°,由平行线的性质可知∠B=∠ADE,∠C=∠AED,然后由翻折的性质可知∠DEF=∠EDF=60°,从而证明∠BDF=∠FEC=60°.
解答 解:∵△ABC为等边三角形,
∴∠B=∠A=∠C=60°.
∵DE∥BC,
∴∠B=∠ADE=60°.
由翻折的性质可知:∠ADE=∠EDF=60°.
∴∠BDF=60°.
∴∠B=∠BDF.
∴BF=FD.
又∵∠B=60°,
∴△BDF为等边三角形.
同理△EFC为等边三角形.
点评 本题主要考查的是翻折的性质、等边三角形的性质和判定、平行线的性质,掌握等边三角形的判定定理是解题的关键.

练习册系列答案
相关题目
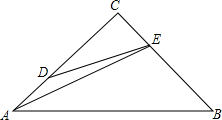 如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.
如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.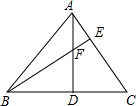 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.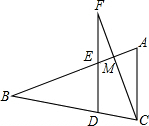 如图,在△ABC中,点D在BC上,过点D作DE∥AC,交AB于点E,延长DE到点F,使EF=DE,连接CF,交AB于点M.
如图,在△ABC中,点D在BC上,过点D作DE∥AC,交AB于点E,延长DE到点F,使EF=DE,连接CF,交AB于点M.