题目内容
8.已知平行四边形ABCD的两条对角线长为8和10,则边AB的取值范围是1<AB<9.分析 由平行四边形的性质得出OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=5,在△AOB中,由三角形的三边关系定理即可得出AB的取值范围.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=5,
在△AOB中,由三角形的三边关系定理得:
5-4<AB<5+4,
即边AB的取值范围是 1<AB<9;
故答案为:1<AB<9.
点评 本题考查了平行四边形的性质、三角形的三边关系定理;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
13. 实数a在数轴上的位置如图所示,则a-1的值是( )
实数a在数轴上的位置如图所示,则a-1的值是( )
 实数a在数轴上的位置如图所示,则a-1的值是( )
实数a在数轴上的位置如图所示,则a-1的值是( )| A. | 1 | B. | -1 | C. | -2 | D. | $\frac{1}{2}$ |
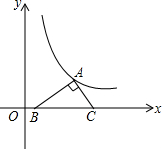 如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.
如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.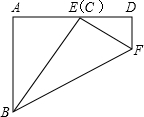 在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19) 如图,是6×6的网格图,任意上下左右相邻的两点间的距离都是1,则以网格图中的格点为顶点画等腰直角三角形,共能画出面积互不相等的等腰直角三角形的个数为( )
如图,是6×6的网格图,任意上下左右相邻的两点间的距离都是1,则以网格图中的格点为顶点画等腰直角三角形,共能画出面积互不相等的等腰直角三角形的个数为( )