题目内容
3.已知:a=$\sqrt{2}$-1,b=$\sqrt{2}$+1,则$\frac{a+\sqrt{ab}}{b+\sqrt{ab}}$=$\sqrt{2}-1$.分析 首先利用平方差公式求得ab的值,然后代入计算即可.
解答 解:ab=($\sqrt{2}$-1)($\sqrt{2}$+1)=($\sqrt{2}$)2-1=2-1=1.
∴原式=$\frac{a+1}{b+1}$=$\frac{\sqrt{2}}{\sqrt{2}+2}$=$\frac{\sqrt{2}(2-\sqrt{2})}{(\sqrt{2}+2)(2-\sqrt{2})}$=$\frac{2\sqrt{2}-2}{2}$=$\sqrt{2}-1$.
故答案为:$\sqrt{2}-1$.
点评 本题主要考查的是根式的化简求值、平方差公式的应用,分母有理化,利用平方差公式化简是解题的关键.

练习册系列答案
相关题目
8.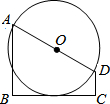 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
 如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )
如图,BC是以AD为直径的⊙O的切线,AB⊥BC,DC⊥BC.在下列哪种情况下,四边形ABCD的面积是整数( )| A. | AB=9,CD=4 | B. | AB=7,CD=3 | C. | AB=5,CD=2 | D. | AB=3,CD=1 |
12.计算:-1+3=( )
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
13. 实数a在数轴上的位置如图所示,则a-1的值是( )
实数a在数轴上的位置如图所示,则a-1的值是( )
 实数a在数轴上的位置如图所示,则a-1的值是( )
实数a在数轴上的位置如图所示,则a-1的值是( )| A. | 1 | B. | -1 | C. | -2 | D. | $\frac{1}{2}$ |
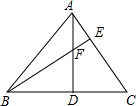 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.