题目内容
8.在不透明的盒子里装有5个分别写有数字0,1,2,3,4的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,然后在剩下的小球中随机再取出一个,将小球上的数字作为点P的纵坐标,则点P落在双曲线y=$\frac{2}{x}$与直线y=-x+5所围成的封闭区域(含边界)的概率是$\frac{1}{2}$.分析 首先根据题意列出表格,然后由表格求得所有等可能的结果和点P落在双曲线y=$\frac{2}{x}$与直线y=-x+5所围成的封闭区域(含边界)的情况数目,再利用概率公式求解即可求得答案.
解答 解:列表得:
| 0 | 4 | 1 | 2 | 3 | |
| 0 | - | 4,2 | 1,0 | 2,0 | 3,0 |
| 4 | 0,4 | - | 1,4 | 2,4 | 3,4 |
| 1 | 0,1 | 4,1 | - | 2,1 | 3,1 |
| 2 | 0,2 | 4,2 | 1,2 | - | 3,2 |
| 3 | 0,3 | 4,3 | 1,3 | 2,3 | - |
∵双曲线y=$\frac{2}{x}$与直线y=-x+5所围成的封闭区域(含边界)x的取值范围是$\frac{5-\sqrt{17}}{2}$<x<$\frac{5+\sqrt{17}}{2}$,
∴共有10种,
∴点P落在双曲线y=$\frac{2}{x}$与直线y=-x+5所围成的封闭区域(含边界)的概率=$\frac{10}{20}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$.
点评 此题考查的是用列表法或树状图法求概率与一次函数的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20.在等边三角形、平行四边形、菱形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
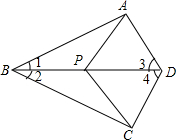 如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.
如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.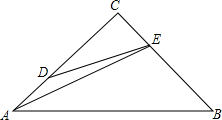 如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.
如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.