题目内容
9.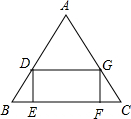 如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;
如图,在△ABC中BC=10,S△ABC=30,矩形DEFG内节接于△ABC,设DE的长为x,(1)写出矩形DEFG面积y与x的函数关系式及定义域;(2)求△ABC内接正方形的面积.
分析 (1)过点A作AH⊥BC于点H,交DG于点K,根据在△ABC中,BC=10,S△ABC=30可得出AG的长,由DE=x,S矩形DEFG=y可知DG=$\frac{y}{x}$,再根据DG∥BC可得出△ADG∽△ABC,由此可得出结论;
(2)根据(1)中y与x的关系式得出DG的长,由正方形的边长相等即可得出结论.
解答  解(1)点A作AH⊥BC于点H,交DG于点K,
解(1)点A作AH⊥BC于点H,交DG于点K,
∵△ABC中BC=10,S△ABC=30,
∴30=$\frac{1}{2}$×10×AH,
解得AH=6.
∵DE=x,S矩形DEFG=y,
∴DG=$\frac{y}{x}$,
∵DG∥BC,
∴△ADG∽△ABC,
∴$\frac{AK}{AH}$=$\frac{DG}{BC}$,即$\frac{AK}{6}=\frac{\frac{y}{x}}{10}$,
解得AK=$\frac{3y}{5x}$,
∴KH=6-$\frac{3y}{5x}$,
∴x=6-$\frac{3y}{5x}$,整理得y=10x-$\frac{5}{3}$x2(0<x<6);
(2)由(1)知y=10x-$\frac{5}{3}$x2=x[10-$\frac{5}{3}$x],
∵矩形DEFG的边长DE=x,
∴边DE的邻边DG=10-$\frac{5}{3}$x
∵当矩形DEFG为正方形时,x=10-$\frac{5}{3}$x,
解得x=$\frac{15}{4}$,
∴当x=$\frac{15}{4}$时,四边形DEFG为正方形,
∴S正方形DEFG=x2=($\frac{15}{4}$)2=$\frac{225}{16}$.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
20.在等边三角形、平行四边形、菱形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
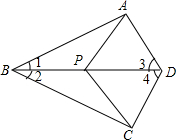 如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.
如图,在四边形ABCD中,点P是对角线BD上任意一点,∠1=∠2,∠3=∠4.求证:PA=PC.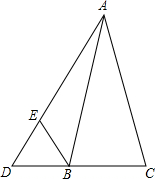 已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.
已知,△ABC中,AB=AC,D是CB延长线上的一点,连接AD,∠ADB=60°,在AD上取一点E使AE=CD,求证:△BDE为等边三角形.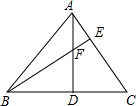 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分为D、E,AD=BD=2,则AF+DC=2.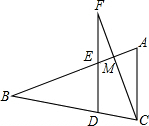 如图,在△ABC中,点D在BC上,过点D作DE∥AC,交AB于点E,延长DE到点F,使EF=DE,连接CF,交AB于点M.
如图,在△ABC中,点D在BC上,过点D作DE∥AC,交AB于点E,延长DE到点F,使EF=DE,连接CF,交AB于点M.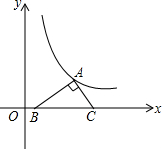 如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.
如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.