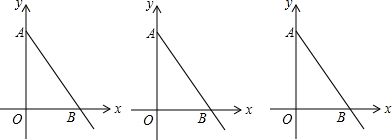题目内容
14.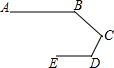 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 90° |
分析 首先过点C作FC∥AB于点F,进而利用平行线的性质得出∠B+∠1+∠2+∠D=360°,即可得出答案.
解答  解:过点C作FC∥AB于点F,
解:过点C作FC∥AB于点F,
由题意可得:AB∥FC∥ED,
则∠B+∠1=180°,∠2+∠D=180°,
故∠B+∠1+∠2+∠D=360°,
即∠B+∠BCD+∠D=360°,
则∠D=360°-140°-100°=120°.
故选:B.
点评 此题主要考查了平行线的性质,灵活应用平行线的性质以及正确作出辅助线是解题关键.

练习册系列答案
相关题目
4.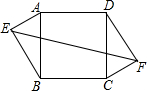 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 14 | B. | 16 | C. | $14\sqrt{2}$ | D. | $14\sqrt{3}$ |
5. 一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
 一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+3的图象如图所示,当y<0时,x的取值范围是( )| A. | x<0 | B. | x>0 | C. | x<2 | D. | x>2 |
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. | 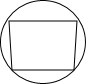 | D. | 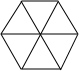 |
9.若a<b,则下列不等式不成立的是( )
| A. | 3a<3b | B. | -3a<-3b | C. | a+3<b+3 | D. | 2a-1<2b-1 |
6.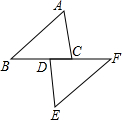 如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
 如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )| A. | AC∥DE | B. | AC=DE | C. | BD=CF | D. | ∠A=∠E |