题目内容
19.如图,平面直角坐标系中,A(0,a),B(b,0),且a、b满足二元一次方程组$\left\{\begin{array}{l}{4a-5b=1}\\{5a-2b=14}\end{array}\right.$,且AB=5.(1)求点A、B坐标.
(2)现有一动点P从点A出发,以每秒2个单位的速度沿射线AB匀速运动,时间为t,线段 BP的长为d,请用含t的式子表示d.
(3)在(2)的条件下,过点B作x轴的垂线交直线OP于点M,当△BOP与△BMP的面积比为3:2时,求t值和点M坐标.
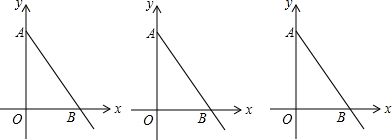
分析 (1)用加减消元法解二元一次方程组$\left\{\begin{array}{l}{4a-5b=1}\\{5a-2b=14}\end{array}\right.$,即可;
(2)分两种情况表示:点P在线段AB上和点P在线段AB的延长线上即可;
(2)分两种情况表示:点P在线段AB上和点P在线段AB的延长线上,利用平行线分线段成比例定理和比例的基本性质即可.
解答 解:(1)∵a、b满足二元一次方程组$\left\{\begin{array}{l}{4a-5b=1}\\{5a-2b=14}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=4}\\{b=3}\end{array}\right.$,
∵A(0,a),B(b,0),
∴A(0,4),B(3,0),
(2)∵一动点P从点A出发,以每秒2个单位的速度沿射线AB匀速运动,时间为t,
∴AP=2t,
①如图1,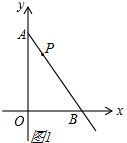
点P在线段AB上时,(0≤t≤$\frac{5}{2}$),
∵AB=5,
∴d=BP=AB-AP=5-2t,
②如图2,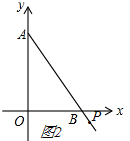
点P在线段AB延长线时,(t>$\frac{5}{2}$),
∵AB=5,
∴d=BP=AP-AB=2t-5,
∴d=$\left\{\begin{array}{l}{5-2t(0≤t≤\frac{5}{2})}\\{2t-5(t>\frac{5}{2})}\end{array}\right.$,
(3)①如图3,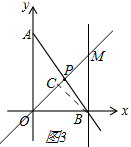
当点P在线段AB上时,过点B作BC⊥OM,
∵过点B作x轴的垂线交直线OP于点M,
∴BM∥OA,
∴$\frac{AP}{PB}=\frac{OP}{PM}$=$\frac{OA}{BM}$,
∵△BOP与△BMP的面积比为3:2,
∴$\frac{\frac{1}{2}OP×BC}{\frac{1}{2}PM×BC}$=$\frac{3}{2}$,
∴$\frac{OP}{PM}=\frac{3}{2}$,
∴$\frac{AP}{PB}=\frac{3}{2}$,
∴$\frac{AP}{AB}=\frac{3}{5}$,
∵AB=5,
∴AP=3,
由(1)有AP=2t,
∴2t=3,
∴t=$\frac{3}{2}$,
∵$\frac{AP}{BP}=\frac{OA}{BM}$=$\frac{3}{2}$,且OA=4,
∴BM=$\frac{8}{3}$,
∴M(3,$\frac{8}{3}$).
方法2,如图5,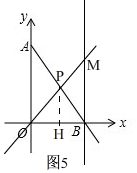
∵S△BOP=$\frac{1}{2}$OB×PH,S△BMP=S△OBM-S△BPO=$\frac{1}{2}$OB×BM-$\frac{1}{2}$OB×PH=$\frac{1}{2}$OB(BM-PH),
∴$\frac{\frac{1}{2}OB×(BM-PH)}{\frac{1}{2}OB×PH}$=$\frac{2}{3}$,
∴$\frac{BM-PH}{PH}=\frac{2}{3}$,
∴$\frac{BM}{PH}=\frac{5}{3}$,
设PH=3a,BM=5a,
∴M(3,5a),
∴直线OM的解析式为y=$\frac{5}{3}$ax
∴当y=3a时,x=$\frac{9}{5}$,
∴H($\frac{9}{5}$,3a),
∵A(0,4),B(3,0),
∴直线AB解析式为y=-$\frac{4}{3}$x+4,
∵点H在直线AB上,
∴-$\frac{4}{3}$×$\frac{9}{5}$+4=3a,
∴a=$\frac{8}{15}$,
∴5a=$\frac{8}{3}$,
∴M(3,$\frac{8}{3}$).
②如图4,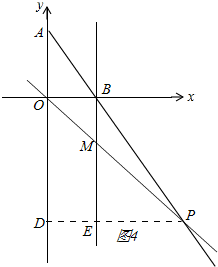
点P在线段AB延长线时,过点P作PD⊥y轴于D,交BM延长线于E,
∴PE∥OB,
∵△BOP与△BMP的面积比为3:2,
∴$\frac{{S}_{△BOP}}{{S}_{△BMP}}=\frac{3}{2}$,
∴$\frac{{S}_{△BOM}}{{S}_{△BMP}}=\frac{1}{2}$,
∴$\frac{\frac{1}{2}BM×OB}{\frac{1}{2}BM×PE}=\frac{1}{2}$,
∴$\frac{OB}{PE}=\frac{1}{2}$
∵B(3,0),
∴OB=3,
∴PE=6,
方法一∵△AOB∽△BEP,
∴$\frac{AB}{BP}=\frac{OB}{PE}$,
∴BP=$\frac{AB×PE}{OB}$=$\frac{5×6}{3}$=10,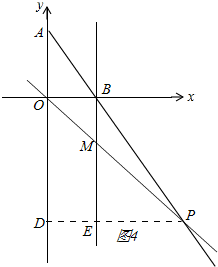
由(1)有,BP=2t-5,
∴2t-5=10,
∴t=$\frac{15}{2}$,
在Rt△BEP中,PB=10,PE=6,
∴BE=8,
∵PE∥OB,
∴$\frac{BM}{ME}=\frac{OB}{PE}=\frac{3}{6}$=$\frac{1}{2}$,
∴$\frac{BM}{BE}=\frac{1}{3}$,
∴BM=$\frac{1}{3}$BE=$\frac{8}{3}$,
∴M(3,-$\frac{8}{3}$).
方法二:
∵OB=3,
∴PD=9,
∵A(0,4),B(3,0),
∴直线AB解析式为y=-$\frac{4}{3}$x+4,
∴P(9,-8),
∴直线OP解析式为y=-$\frac{8}{9}$x,
当x=3时,y=-$\frac{8}{3}$,
∴M(3,-$\frac{8}{3}$)
点评 此题是三角形综合题,主要考查了二元一次方程组的解法,平行线分线段成比例定理,比例的基本性质,解本题的关键是用同底的两个三角形面积比等于高的比.

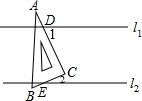 如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )
如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )| A. | 15° | B. | 25° | C. | 30° | D. | 35° |
| A. | 1:4 | B. | 1:8 | C. | 1:16 | D. | 1:2 |
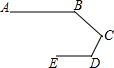 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 90° |
 如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )| A. | x+y+z=180° | B. | x+y-z=180° | C. | y-x-z=0° | D. | y-x-2z=0° |
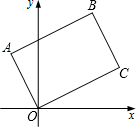 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )| A. | (4,2) | B. | (2,4) | C. | ($\frac{3}{2}$,3) | D. | (3,$\frac{3}{2}$) |
 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 正三棱柱 | D. | 正三棱锥 |