题目内容
4.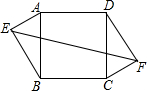 如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )
如图,在正方形ABCD中,AD=10,点E、F是正方形ABCD外的点,且AE=FC=6,BE=DF=8,则EF的长为( )| A. | 14 | B. | 16 | C. | $14\sqrt{2}$ | D. | $14\sqrt{3}$ |
分析 延长EA交FD的延长线于点M,可证明△EMF是等腰直角三角形,而EM=MF=AE+DF=14,所以利用勾股定理即可求出EF的长.
解答 解:
延长EA交FD的延长线于点M,
∵四边形ABCD是正方形,
∴AB=BC=DC=AD=10,
∵AE=6,BE8,
∴AE2+BE2=AB2=100,
∴△AEB是直角三角形,
同理可证△CDF是直角三角形,
∴∠EAB=∠DCF,∠EBA=∠CDF,∠EAB+∠EBA=90°,∠CDF+∠FDC=90°,
∴∠EAB+∠CDF=90°
又∵∠EAB+∠MAD=90°,∠MDA+∠CDF=90°,
∴∠MAD+∠MDA=90°,
∴∠M=90°
∴△EMF是直角三角形,
∵∠EAB+∠MAD=90°,
∴∠EAB=∠MDA,
在△AEB和△DMA中,
$\left\{\begin{array}{l}{∠AEB=∠M=90°}\\{∠EAB=∠MDA}\\{AB=AD}\end{array}\right.$,
∴△AEB≌△DMA,
∴AM=BE=8,MD=AE=6,
∴EM=MF=14,
∴EF=$\sqrt{M{E}^{2}+M{F}^{2}}$=14$\sqrt{2}$,
故选C.
点评 本题考查了正方形的性质、全等三角形的判定和性质以及勾股定理的运用,题目的综合性较强,难度中等,是一道非常不错的中考题目,证明出三角形△EMF是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
15.如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
| A. | (-1,2) | B. | (-1,-1) | C. | (-1,1) | D. | (1,1) |
12.若不等式组$\left\{\begin{array}{l}2x-4≤0\\ 1+x>a\end{array}\right.$有解,则a的取值范围是( )
| A. | a≤3 | B. | a<3 | C. | a<2 | D. | a≤2 |
9.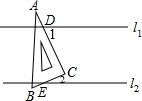 如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )
如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )
 如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )
如图,直线l1∥l2,一直角三角板ABC(∠ACB=90°)放在平行线上,两直角边分别与l1、l2交于点D、E,现测得∠1=75°,则∠2的度数为( )| A. | 15° | B. | 25° | C. | 30° | D. | 35° |
16.若a<b,则下列不等式中成立的是( )
| A. | a-b>0 | B. | a-2<b-2 | C. | $\frac{1}{2}$a>$\frac{1}{2}$b | D. | -2a<-2b |
 如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )
如图是一个由6个相同的小立方体组成的几何体,从上面看得到的平面图形是( )



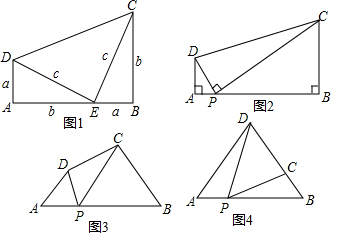 如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果:
如图1是美国第20届总统加菲尔德于1876年公开发表的勾股定理一个简明证法,聪明的思齐和他的社团小朋友们发现:两个直角三角形在发生变化过程中,只要满足一定的条件,就会有神奇的结果: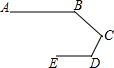 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )