题目内容
6.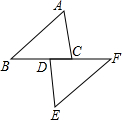 如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )
如图,已知AB∥EF,AB=EF,则下列条件中,不能作为判断△ABC≌△EFD的是( )| A. | AC∥DE | B. | AC=DE | C. | BD=CF | D. | ∠A=∠E |
分析 根据全等三角形的判定方法依次判断即可.
解答 解:
∵AB∥EF,
∴∠B=∠F,且AB=EF,
当AC∥DE时,可得∠ACB=∠EDF,在△ABC和△EFD中,满足AAS,故A可以判定;
当AC=DE时,在△ABC和△EFD中,满足SSA,故B不可以判定;
当BD=CF时,可得BC=DF,在△ABC和△EFD中,满足SAS,故C可以判定;
当∠A=∠E时,在△ABC和△EFD中,满足ASA,故D可以判定;
故选B.
点评 本题主要考查三角形全等的判定方法,掌握全等三角形的五种判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
16.若a<b,则下列不等式中成立的是( )
| A. | a-b>0 | B. | a-2<b-2 | C. | $\frac{1}{2}$a>$\frac{1}{2}$b | D. | -2a<-2b |
17. 如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
 如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )| A. | 20cm | B. | 18cm | C. | 16cm | D. | 10cm |
14.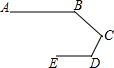 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 90° |
1.下列计算错误的是( )
| A. | 5$\sqrt{0.2}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
11.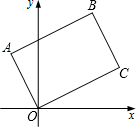 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )| A. | (4,2) | B. | (2,4) | C. | ($\frac{3}{2}$,3) | D. | (3,$\frac{3}{2}$) |
15. 如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
 如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )| A. | 60° | B. | 30° | C. | 120° | D. | 50° |
16.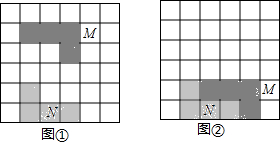 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )| A. | 向右平移2个单位,向下平移3个单位 | |
| B. | 向右平移1个单位,向下平移3个单位 | |
| C. | 向右平移1个单位,向下平移4个单位 | |
| D. | 向右平移2个单位,向下平移4个单位 |