题目内容
16.(1)计算:|-2|+(2-π)0-4×${2}^{-2}-(2\sqrt{2})$2.(2)解方程:x2+4x-2=0.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算,最后一项利用平方根定义计算即可得到结果;
(2)方程利用配方法求出解即可.
解答 解:(1)原式=2+1-1-8=3-9=-6;
(2)方程整理得:x2+4x=2,
配方得:x2+4x+4=6,即(x+2)2=6,
开方得:x+2=±$\sqrt{6}$,
解得:x1=-2+$\sqrt{6}$,x2=-2-$\sqrt{6}$.
点评 此题考查了实数的运算,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.函数y=$\frac{3}{\sqrt{x+2}}$中,自变量x的取值范围是( )
| A. | x≠-2 | B. | x≥-2 | C. | x>-2 | D. | x>2 |
6.下列运算正确的是( )
| A. | x2+x3=x5 | B. | ($\frac{x}{y}$)2=$\frac{{x}^{2}}{y}$ | C. | x2•x3=x6 | D. | (x2)3=x6 |
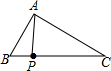
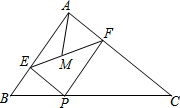 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.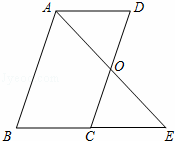 已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.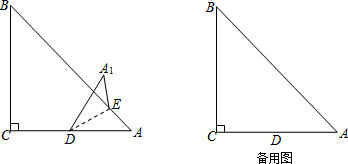
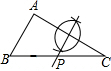
 如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )
如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )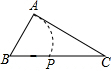

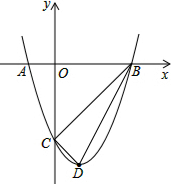 如图,抛物线y=x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),点D为顶点,连接BC、BD、CD.
如图,抛物线y=x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),点D为顶点,连接BC、BD、CD.