Question

1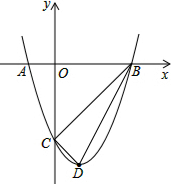．如图，抛物线y=x²+bx+c与x轴交于A、B（3，0）两点，与y轴交于点C（0，-3），点D为顶点，连接BC、BD、CD．
（1）求抛物线的表达式；
（2）试判断△BCD的形状，并说明理由；
（3）将该抛物线平移，使它的顶点P与点A关于直线BD对称，求点P的坐标并写出平移的方法．

Answer 1

分析 （1）由点B和点C的坐标可求得b、c的值，从而得到抛物线的表达式；
（2）线求得点D的坐标，然后可求得CD、BD、BC，最后依据勾股定理的逆定理可证明△CDB为直角三角形；
（3）如图2所示．作点A关于直线BD的对称点P交BD于点M．先求得点A的坐标，然后求得BD的解析式，从而得到直线PA的一次项系数，然后由点A的坐标可求得AP的解析式，将AP的解析式与BD的解析式联立可求得点M的坐标，然后由中点坐标公式可求得点P的坐标，由点P的坐标可判断出抛物线平移的方向和距离．

解答 解：（1）∵抛物线y=x2+bx+c经过点B（3，0），点C（0，-3），
∴$\left\{\begin{array}{l}{9+3b+c=0}\\{c=-3}\end{array}\right.$，解得：b=-2，C=-3．
∴抛物线的表达式为y=x²-2x-3．
（2）△BCD是直角三角形．
理由如下：如图1所示：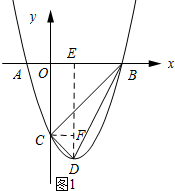

∵点B的坐标为（3，0），点C的坐标为（0，-3），
∴OB=OC=3．
在Rt△COB中，∠BOC=90°，
∴BC²=OB²+OC²=18．
过点D作DE⊥x轴与点E．
由y=x²-2x-3=（x-1）²-4，得顶点D的坐标为（1，-4）．
∴DE=4，OE=1．
∴BE=2．
在Rt△DEB中，∠DEB=90°，
∴BD²=DE²+BE²=20．
过点C作CF⊥DE于点F，则CF=OE=1，DF=DE-OC=1．
∴DC²=CF²+DF²=2．
∴BD²=BC²+DC²．
∴△BCD是直角三角形．
（3）如图2所示．作点A关于直线BD的对称点P交BD于点M．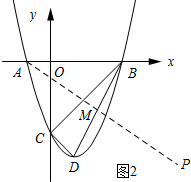

当y=0时，x²-2x-3=0．解得：x₁=3，x₂=-1．
∴A（-1，0）．
设BD的解析式为y=kx+b．
∵将D（1，-4），B（3，0）代入得；$\left\{\begin{array}{l}{k+b=-4}\\{3k+b=0}\end{array}\right.$，解得：k=2，b=-6，
∴直线BD的解析式为y=2k-6．
∵AP与BD垂直，
∴直线AP的一次项系数为-$\frac{1}{2}$．
设直线AP的解析式为y=-$\frac{1}{2}x$+n．
∵将A（-1，0）代入得：$\frac{1}{2}$+n=0，解得n=-$\frac{1}{2}$，
∴直线AP的解析式为y=-$\frac{1}{2}x$$-\frac{1}{2}$．
∵将y=$-\frac{1}{2}$x$-\frac{1}{2}$与y=2x-6联立，解得：x=$\frac{11}{5}$，y=-$\frac{8}{5}$．
∴点M的坐标为（$\frac{11}{5}$，-$\frac{8}{5}$）．
由轴对称的性质可知：M是AP的中点，
∴点P的坐标为（$\frac{27}{5}$，-$\frac{16}{5}$）．
∵抛物线y=（x-1）²-4平移后的顶点坐标为P，
∴抛物线y=x-1）²-4先向右平移$\frac{22}{5}$个单位长度，再向上平移$\frac{4}{5}$个单位长度所得抛物线的顶点与点A关于BD对称．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、二次函数的顶点坐标、勾股定理的逆定理的应用、翻折的性质、相互垂直的两条直线的特点、直线的中点坐标公式，明确相互垂直的两条直线的一次项系数的乘积为-1是解题的关键．