题目内容
13. 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
分析 作PM⊥BC于M,作PN⊥CD于N,则∠PMB=∠PMC=∠PNE=90°,证明四边形PMCN是正方形,得出MC=CN,PM=PN,∠MPN=90°,PC=$\sqrt{2}$MC,由ASA证明△BPM≌△EPN,得出BM=EN,得出BC+CE=MC+CN=2MC,即可得出结论.
解答 证明:作PM⊥BC于M,作PN⊥CD于N,如图所示:
则∠PMB=∠PMC=∠PNE=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ACB=∠ACD=45°,
∴四边形PMCN是矩形,PM=PN,
∴四边形PMCN是正方形,
∴MC=CN,PM=PN,∠MPN=90°,PC=$\sqrt{2}$MC,
∵PE⊥BP,
∴∠BPE=90°,
∴∠BPM=∠EPN,
在△BPM和△EPN中,
$\left\{\begin{array}{l}{∠PMB=∠PNE}&{\;}\\{PM=PN}&{\;}\\{∠BPM=∠EPN}&{\;}\end{array}\right.$,
∴△BPM≌△EPN(ASA),
∴BM=EN,
∴BC+CE=BM+MC+CE=EN+CE+MC=MC+CN=2MC,
∴$\frac{BC+CE}{PC}$=$\frac{2MC}{\sqrt{2}MC}$=$\sqrt{2}$.
点评 本题考查了正方形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 在直径为100cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=80cm,求油的最大深度.
在直径为100cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=80cm,求油的最大深度. 如图,以A为圆心,AD长为半径作⊙A,P为$\widehat{BD}$上的动点,连PD交⊙A于Q,K为PQ中点,求定长HK.
如图,以A为圆心,AD长为半径作⊙A,P为$\widehat{BD}$上的动点,连PD交⊙A于Q,K为PQ中点,求定长HK.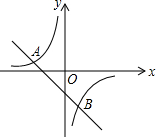 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.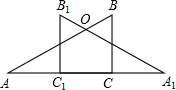 两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.
两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.