题目内容
3.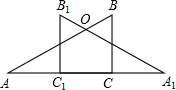 两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.
两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线.(1)问图中有多少对相似三角形,多少对全等三角形?并将它们写出来;
(2)选出其中一对相似三角形进行证明.
分析 (1)利用30°、60°和90°和相似三角形的判定方法可判断图中有7组相似三角形,根据全等三角形的判定方法图中有3对全等三角形;
(2)利用与三角形一边平行的直线截其它两边所得的三角形与原三角形相似可判断△AC1D∽△ACB.
解答 解: (1)相似三角形有:△AC1D∽△ACB,△AC1D∽△A1C1B1,△AC1D∽△A1C1B1,△AC1D∽△A1CE,△A1CE∽△A1C1B1,△A1CE∽△ACB,
(1)相似三角形有:△AC1D∽△ACB,△AC1D∽△A1C1B1,△AC1D∽△A1C1B1,△AC1D∽△A1CE,△A1CE∽△A1C1B1,△A1CE∽△ACB,
△ODB1∽△OEB;全等三角形有:△ACB∽△A1C1B1,△AC1D≌△A1CE,△A1CE∽△A1C1B1,△ODB1≌△OEB;
(2)∵DC1∥BC,
∴△AC1D∽△ACB.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了全等三角形的判定.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
11.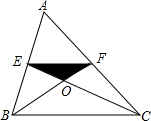 如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
 如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
12.已知?ABCD,AC、BD是对角线,下列结论中不一定正确的是( )
| A. | AB=CD | B. | AC=BD | ||
| C. | AC⊥BD时,它是菱形 | D. | AD∥BC |
 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.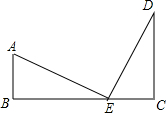 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.
如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.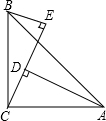 已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.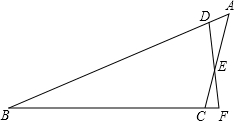 已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.
已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.