题目内容
2.平行四边形ABCD的周长是56cm,对角线AC、BD相交于点O,△OAB与△OBC的周长差是4cm,则平行四边形ABCD中较短的边长是12cm.分析 由平行四边形ABCD的周长是56cm,可得AB+BC=28cm,又由△OAB与△OBC的周长差是4cm,可得AB-BC=4cm,继而求得答案.
解答 解:∵平行四边形ABCD的周长是56cm,
∴AB+BC=28cm,OA=OC,
∵△OAB与△OBC的周长差是4cm,
∴(OA+OB+AB)-(OB+OC+BC)=AB-BC=4cm,
∴$\left\{\begin{array}{l}{AB+BC=28cm}\\{AB-BC=4cm}\end{array}\right.$,
∴AB=16cm,BC=12cm.
∴平行四边形ABCD中较短的边长是12cm.
故答案为:12cm.
点评 此题考查了平行四边形的性质.注意根据题意得到方程组是关键.

练习册系列答案
相关题目
11.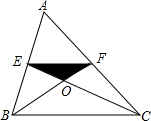 如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
 如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )
如图,在△ABC中,E、F分别为边AB、AC的中点,连接CE、BF,交点为O,△AEF的面积为1,那么△EOF的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
12.已知?ABCD,AC、BD是对角线,下列结论中不一定正确的是( )
| A. | AB=CD | B. | AC=BD | ||
| C. | AC⊥BD时,它是菱形 | D. | AD∥BC |
 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.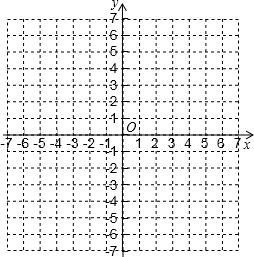 在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).
在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).
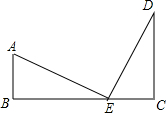 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.
如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.