题目内容
3. 在直径为100cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=80cm,求油的最大深度.
在直径为100cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=80cm,求油的最大深度.
分析 先连接OA,过点O作OC⊥AB,交⊙O于D,根据垂径定理,即可求得AC的值,然后在Rt△OAC中,利用勾股定理,即可求得OC的值,继而求得油的最大深度.
解答  解:如图,过O作OC⊥AB于点C,并延长交⊙O于点D,连结OA,
解:如图,过O作OC⊥AB于点C,并延长交⊙O于点D,连结OA,
依题意得CD就是油的最大深度,
根据垂径定理得:AC=$\frac{1}{2}$AB=40cm,OA=50cm,…(6分)
在Rt△OAC中,根据勾股定理得:OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{5{0}^{2}-4{0}^{2}}$=30(cm),
∴CD=OD-OC=50-30=20(cm),
答:油的最大深度是20cm.
点评 此题考查了垂径定理的应用.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
18.在10分钟的时间内,分针转过的角度是( )
| A. | 15° | B. | 30° | C. | 15° | D. | 60° |
8.一个等腰三角形的顶角等于40°,则这个等腰三角形的底角度数是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )
如图的几何体,是由一个圆柱体从正中央挖去了一个与它等高的长方体后形成的,其俯视图如下,这个几何体的主视图是( )



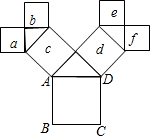 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形ABCD的边长为6,则正方形a,b,c,d,e,f的面积和为72.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形ABCD的边长为6,则正方形a,b,c,d,e,f的面积和为72. 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.