题目内容
18.⊙O1和⊙O2相交于A,B两点,⊙O1的半径为10,⊙O2的半径为17,AB=16,则两圆的圆心距为21或9.分析 连接AO1,AO2,由勾股定理可以分别求出O1P和O2P,分两种情况求出结论.
解答  解:连接AO1,AO2,
解:连接AO1,AO2,
∴AO1=10,AO2=17,
∵AB=16,
∴AP=8,∠APO1=∠APO2=90°.
在Rt△APO1和Rt△APO2中,由勾股定理,得
PO1=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
PO2=$\sqrt{1{7}^{2}-{8}^{2}}$=15,
∴O1O2=15+6=21,
或O1O2=15-6=9.
故答案为:21或9.
点评 本题考查了相交两圆的性质和勾股定理的运用,解答时灵活作出辅助线、运用相交两圆的连心线垂直平分公共弦和勾股定理是解答本题的关键,注意分情况讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个等腰三角形的顶角等于40°,则这个等腰三角形的底角度数是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
9.已知:⊙O1、⊙O2的半径分别为3和6,且圆心距O1O2=3,则这两圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |
 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.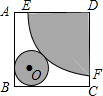 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.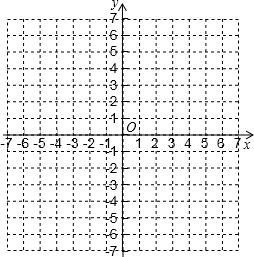 在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).
在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).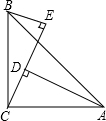 已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.
已知:如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,求BE的长.