题目内容
5.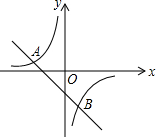 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$图象交于A(-2,1),B(1,n)两点.(1)此反比例函数的解析式是y=-$\frac{2}{x}$,n=-2;
(2)根据图象可得一次函数的值大于反比例函数的值的x的取值范围是x<-2或0<x<1.
分析 (1)根据反比例函数y=$\frac{m}{x}$图象过点A(-2,1),利用待定系数法求出即可;把B(1,n)代入解析式求得n的值;
(2)根据图象即可求得.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$图象经过A(-2,1),
∴m=-2×1=-2.
∴反比例函数的解析式为y=-$\frac{2}{x}$.
∴B(1,n)在y=-$\frac{2}{x}$上,所以n=-$\frac{2}{1}$=-2.
故答案为y=-$\frac{2}{x}$,-2.
(2)A(-2,1),B(1,-2),
由图象可知:x<-2或0<x<1.
故答案为x<-2或0<x<1.
点评 此题主要考查了待定系数法求出反比例函数、一次函数解析式以及求不等式和函数的关系,熟练掌握待定系数法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.猜数字游戏:小明手里有分别标有正整数的四张卡片,小明将四张卡片洗匀后,背面朝上放在桌上,由小刚蒙眼每次抽取两张,并由小明将数字和记录下来后放回,然后重复上面的游戏.当所有可能的数字和都已出现后,小刚猜出了卡片上的数字.如表是小明记录数字和出现的次数统计表:
(1)在表中,数字和为8出现的频率是多少?
(2)猜猜卡片上的数字有哪些?
(3)求数字和为偶数的概率.
| 数字和 | 5 | 7 | 8 | 9 | 11 |
| 出现次数 | 8 | 10 | 22 | 9 | 11 |
(2)猜猜卡片上的数字有哪些?
(3)求数字和为偶数的概率.
 如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.
如图,在正方形ABCD中,点P为直线AC上一点,连接BP,过P作PE⊥BP交直线CD于E.试证明:$\frac{BC+CE}{PC}$=$\sqrt{2}$.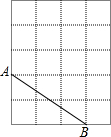 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.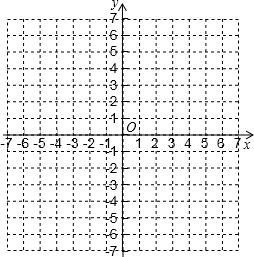 在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).
在如图的平面直角坐标系中表示下面各点,并在图中标上字母:A(0,3);B(-2,4);C(3,-4);D(-3,-4).
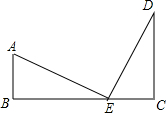 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.
如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC.试探索线段AB、CD、BC之间的数量关系,请你写出关系式并证明.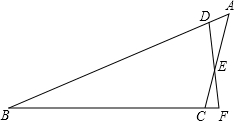 已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.
已知:如图,在△ABC中,AB=20,BC=16,AC=8,点D、E分别在边AB、AC上,且AD=2,AE=5,DE与BC的延长线相交于点F.求△CEF的各边长.