题目内容
6.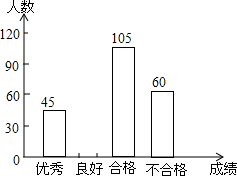 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
分析 (1)利用合格的人数除以该组频率进而得出该校初四学生总数;
(2)利用(1)中所求,结合频数÷总数=频率,进而求出答案;
(3)根据题意画出树状图,然后求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率.
解答  解:(1)由题意可得:该校初四学生共有:105÷0.35=300(人),
解:(1)由题意可得:该校初四学生共有:105÷0.35=300(人),
答:该校初四学生共有300人;
(2)由(1)得:a=300×0.3=90(人),
b=$\frac{45}{300}$=0.15,
c=$\frac{60}{300}$=0.2;
如图所示;
(3)画树形图得:
∴一共有12种情况,抽取到甲和乙的有2种,
∴P(抽到甲和乙)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题主要考查了树状图法求概率以及条形统计图的应用,根据题意利用树状图得出所有情况是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
14.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则下列结论错误的是( )
| A. | 方差是8 | B. | 极差是9 | C. | 众数是-1 | D. | 平均数是-1 |
11.已知$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}mx+ny=8\\ nx-my=1\end{array}\right.$的解,则2m-n的平方根为( )
| A. | ±2 | B. | $\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | 2 |
18.南宁快速公交(简称:BRT)将在今年底开始动工,预计2016年下半年建成并投入试运营,首条BRT西起南宁火车站,东至南宁东站,全长约为11300米,其中数据11300用科学记数法表示为( )
| A. | 0.113×105 | B. | 1.13×104 | C. | 11.3×103 | D. | 113×102 |
 如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F. 如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.
如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.