题目内容
14.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则下列结论错误的是( )| A. | 方差是8 | B. | 极差是9 | C. | 众数是-1 | D. | 平均数是-1 |
分析 分别计算该组数据的平均数,众数,极差及方差后找到正确的答案即可.
解答 解:根据题意可知x=-1,
平均数=(-6-3-1-1+2+3)÷6=-1,
∵数据-1出现两次最多,
∴众数为-1,
极差=3-(-6)=9,
方差=$\frac{1}{6}$[(-6+1)2+(-3+1)2+(-1+1)2+(2+1)2+(-1+1)2+(3+1)2]=9.
故选A.
点评 此题考查了方差、极差、平均数、中位数及众数的知识,属于基础题,掌握各部分的定义及计算方法是解题关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
4.某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
表2
(1)在表2中,a=8,b=7.5;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
表1
| 一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
| 二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
| 班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
| 一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
| 二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
5.下列运算正确的是( )
| A. | (a2)5=a7 | B. | a2•a4=a6 | C. | 3a2b-3ab2=0 | D. | ($\frac{a}{2}$)2=$\frac{{a}^{2}}{2}$ |
2. 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
9.将数字2.03×10-3化为小数是( )
| A. | 0.203 | B. | 0.0203 | C. | 0.00203 | D. | 0.000203 |
6.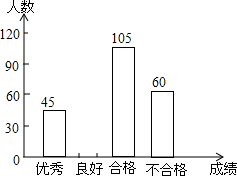 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
(1)该校初四学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
3.下列运算正确的是( )
| A. | 4ab÷2a=2ab | B. | (3x2)3=9x6 | C. | a3•a4=a7 | D. | $\sqrt{6}÷\sqrt{3}=2$ |
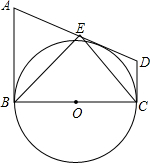 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )