题目内容
11.已知$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}mx+ny=8\\ nx-my=1\end{array}\right.$的解,则2m-n的平方根为( )| A. | ±2 | B. | $\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | 2 |
分析 由x=2,y=1是二元一次方程组的解,将x=2,y=1代入方程组求出m与n的值,进而求出2m-n的值,利用平方根的定义即可求出2m-n的平方根.
解答 解:∵将$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$代入$\left\{\begin{array}{l}mx+ny=8\\ nx-my=1\end{array}\right.$中,得:$\left\{\begin{array}{l}{2m+n=8}\\{2n-m=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=3}\\{n=2}\end{array}\right.$
∴2m-n=6-2=4,
则2m-n的平方根为±2.
故选:A.
点评 此题考查了二元一次方程组的解,以及平方根的定义,解二元一次方程组的方法有两种:加减消元法;代入消元法.

练习册系列答案
相关题目
2. 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
 如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{28}{5}$.
6.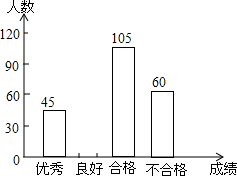 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
(1)该校初四学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(2)求表中a,b,c的值,并补全条形统计图.
(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
16.(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为(1,4),点C的坐标为(0,3).
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
3.下列运算正确的是( )
| A. | 4ab÷2a=2ab | B. | (3x2)3=9x6 | C. | a3•a4=a7 | D. | $\sqrt{6}÷\sqrt{3}=2$ |

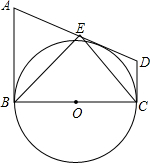 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( ) 看图找规律,“?”处应填-10.
看图找规律,“?”处应填-10. 如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.
如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.