题目内容
8.下列命题正确的是( )| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 两边及其一角相等的两个三角形全等 | |
| C. | 16的平方根是4 | |
| D. | 一组数据2,0,1,6,6的中位数和众数分别是2和6 |
分析 根据平行四边形的判定定理、三角形全等的判定定理、平方根的概念、中位数和众数的概念进行判断即可.
解答 解:A.一组对边平行,另一组对边相等的四边形不一定是平行四边形,故错误;
B.两边及其一角相等的两个三角形不一定全等,故错误;
C.16的平方根是±4,故错误,
D.一组数据2,0,1,6,6的中位数和众数分别是2和6,故正确,
故选:D.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
18. 如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )
如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )
 如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )
如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )| A. | $\frac{7}{4}$ | B. | 3 | C. | $\frac{15}{4}$ | D. | 4 |
13.下列运算正确的是( )
| A. | a+2a=2a2 | B. | (-2ab2)2=4a2b4 | C. | a6÷a3=a2 | D. | (a-3)2=a2-9 |
18.下列算式
①$\sqrt{9}$=±3;②${(-\frac{1}{3})}^{-2}$=9;③26÷23=4;④$(\sqrt{-2016})^2$=2016;⑤a+a=a2.
运算结果正确的概率是( )
①$\sqrt{9}$=±3;②${(-\frac{1}{3})}^{-2}$=9;③26÷23=4;④$(\sqrt{-2016})^2$=2016;⑤a+a=a2.
运算结果正确的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
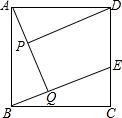 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.