题目内容
19.杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: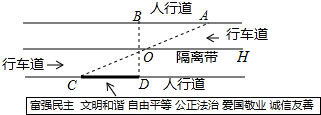
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
分析 由AB∥CD,利用平行线的性质可得∠ABO=∠CDO,由垂直的定义可得∠CDO=90°,易得OB⊥AB,由相邻两平行线间的距离相等可得OD=OB,利用ASA定理可得
△ABO≌△CDO,由全等三角形的性质可得结果.
解答 解:∵AB∥CD,∴∠ABO=∠CDO,
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,即OB⊥AB,
∵相邻两平行线间的距离相等,
∴OD=OB,
在△ABO与△CDO中,
$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{OB=OD}\\{∠AOB=∠COD}\end{array}\right.$,
∴△ABO≌△CDO(ASA),
∴CD=AB=20(m)
点评 本题主要考查了平行线的性质和全等三角形的判定及性质定理,综合运用各定理是解答此题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
9.若单项式2x3ya+b与-$\frac{1}{3}$xa-by5是同类项,则a,b的值分别为( )
| A. | a=-4,b=-1 | B. | a=-4,b=1 | C. | a=4,b=-1 | D. | a=4,b=1 |
10.下列计算中,正确的是( )
| A. | x2+x3=x5 | B. | (x2)5=(-x5)2 | C. | (x3y2)3=x6y5 | D. | x2•x3=x6 |
14.下列计算中正确的是( )
| A. | 2a•3a=6a | B. | (a2)3=a5 | C. | (a+3)2=a2+9 | D. | (-3a)-2=$\frac{1}{9{a}^{2}}$ |
4.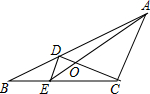 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
11.下列说法正确的是( )
| A. | 长方体的截面一定是长方形 | |
| B. | 了解一批日光灯的使用寿命适合采用的调查方式是普查 | |
| C. | 一个圆形和它平移后所得的圆形全等 | |
| D. | 多边形的外角和不一定都等于360° |
8.下列命题正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 两边及其一角相等的两个三角形全等 | |
| C. | 16的平方根是4 | |
| D. | 一组数据2,0,1,6,6的中位数和众数分别是2和6 |
9. 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )
 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是(3,0).
如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是(3,0).