题目内容
18．
如图，△ABC是一张纸片，∠C=90°，AC=6，BC=8，现将其折叠．使点B与点A重合，折痕为DE，则DE的长为（ ）| A． | $\frac{7}{4}$ | B． | 3 | C． | $\frac{15}{4}$ | D． | 4 |
分析 直接利用勾股定理得出AB的长，再利用相似三角形的判定与性质得出DE的长．
解答 解：如图所示：∵∠C=90°，AC=6，BC=8，
∴AB=10，
∵现将其折叠．使点B与点A重合，折痕为DE，
∴AE=BE=5，
∵∠DEB=∠C=90°，∠B=∠B，
∴△BDE∽△BAC，
∴$\frac{BE}{BC}$=$\frac{DE}{AC}$，
即$\frac{5}{8}$=$\frac{DE}{6}$，
解得：DE=$\frac{15}{4}$．
故选：C．
点评 此题主要考查了翻折变换的性质以及相似三角形的判定与性质、勾股定理等知识，正确得出△BDE∽△BAC是解题关键．
练习册系列答案
相关题目
8．下列图形中，既是轴对称图形又是中心对称图形的有（ ）
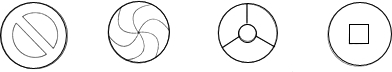
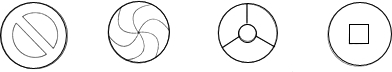
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．若单项式2x3ya+b与-$\frac{1}{3}$xa-by5是同类项，则a，b的值分别为（ ）
| A． | a=-4，b=-1 | B． | a=-4，b=1 | C． | a=4，b=-1 | D． | a=4，b=1 |
6．下列运算正确的是（ ）
| A． | （-1）0=0 | B． | $\sqrt{1}$=±1 | C． | $\root{3}{-1}$=1 | D． | 3-1=$\frac{1}{3}$ |
13．计算（-6）÷2的结果等于（ ）
| A． | -4 | B． | -3 | C． | 3 | D． | -12 |
3．若关于x的方程$\frac{x+m}{x-3}$+$\frac{3m}{3-x}$=3的解为正数，则m的取值范围是（ ）
| A． | m＜$\frac{9}{2}$ | B． | m＜$\frac{9}{2}$且m≠$\frac{3}{2}$ | C． | m＞-$\frac{9}{4}$ | D． | m＞-$\frac{9}{4}$且m≠-$\frac{3}{4}$ |
10．下列计算中，正确的是（ ）
| A． | x2+x3=x5 | B． | （x2）5=（-x5）2 | C． | （x3y2）3=x6y5 | D． | x2•x3=x6 |
如图是利用网格画出的太原市地铁1，2，3号线路部分规划示意图，若建立适当的平面直角坐标系，表示双塔西街点的坐标为（0，-1），表示桃园路的点的坐标为（-1，0），则表示太原火车站的点（正好在网格点上）的坐标是（3，0）．
8．下列命题正确的是（ ）
| A． | 一组对边平行，另一组对边相等的四边形是平行四边形 | |
| B． | 两边及其一角相等的两个三角形全等 | |
| C． | 16的平方根是4 | |
| D． | 一组数据2，0，1，6，6的中位数和众数分别是2和6 |