题目内容
20.已知一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C,且AB=2BC,则这个反比例函数的表达式为y=$\frac{6}{x}$.分析 根据已知条件得到A(-2,0),B(0,4),过C作CD⊥x轴于D,根据相似三角形的性质得到$\frac{OB}{CD}=\frac{AO}{AD}$=$\frac{AB}{AC}$=$\frac{2}{3}$,求得C(1,6),即可得到结论.
解答 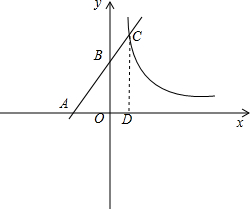 解:∵一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,
解:∵一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,
∴A(-2,0),B(0,4),
过C作CD⊥x轴于D,
∴OB∥CD,
∴△ABO∽△ACD,
∴$\frac{OB}{CD}=\frac{AO}{AD}$=$\frac{AB}{AC}$=$\frac{2}{3}$,
∴CD=6,AD=3,
∴OD=1,
∴C(1,6),
设反比例函数的解析式为y=$\frac{k}{x}$,
∴k=6,
∴反比例函数的解析式为y=$\frac{6}{x}$.
故答案为:y=$\frac{6}{x}$.
点评 本题考查了反比例函数与一次函数的交点,相似三角形的判定和性质,求函数的解析式,正确的作出图形是解题的关键.

练习册系列答案
相关题目
10.下列计算中,正确的是( )
| A. | x2+x3=x5 | B. | (x2)5=(-x5)2 | C. | (x3y2)3=x6y5 | D. | x2•x3=x6 |
11.下列说法正确的是( )
| A. | 长方体的截面一定是长方形 | |
| B. | 了解一批日光灯的使用寿命适合采用的调查方式是普查 | |
| C. | 一个圆形和它平移后所得的圆形全等 | |
| D. | 多边形的外角和不一定都等于360° |
8.下列命题正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 两边及其一角相等的两个三角形全等 | |
| C. | 16的平方根是4 | |
| D. | 一组数据2,0,1,6,6的中位数和众数分别是2和6 |
15. 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 12cm | B. | 6cm | C. | 3$\sqrt{2}$cm | D. | 2$\sqrt{3}$cm |
9. 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )
 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
 昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象. 若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=-2x2+4x+2与C2:y2=-x2+mx+n为“友好抛物线”.
若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=-2x2+4x+2与C2:y2=-x2+mx+n为“友好抛物线”.