题目内容
16.如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知$\frac{AC}{BD}=2$,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
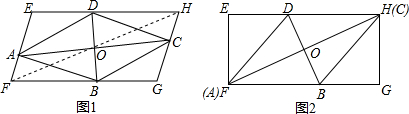
分析 (1)根据菱形的性质可得出OA=OC,OD=OB,再由中点的性质可得出OF=OH,结合对顶角相等即可利用全等三角形的判定定理(SAS)证出△AOF≌△COH,从而得出AF∥CH,同理可得出DH∥BF,依据平行四边形的判定定理即可证出结论;
(2)设BD=m(m>0),则AC=2m,结合矩形的面积为20即可求出m=2$\sqrt{5}$,进而得出AC、BD的长度,再由勾股定理即可得出AB的长度,由四边形EFGH为矩形即可得出△AOB∽△AGC,根据相似比即可得出$\frac{OB}{CG}=\frac{OA}{AG}=\frac{AB}{AC}$,代入数据,此题得解.
解答 (1)证明:∵点O是菱形ABCD对角线AC、BD的交点,
∴OA=OC,OD=OB,
∵点O是线段FH的中点,
∴OF=OH.
在△AOF和△COH中,有$\left\{\begin{array}{l}{OA=OC}\\{∠AOF=∠COH}\\{OF=OH}\end{array}\right.$,
∴△AOF≌△COH(SAS),
∴∠AFO=∠CHO,
∴AF∥CH.
同理可得:DH∥BF.
∴四边形EFGH是平行四边形.
(2)设BD=m,则AC=2m,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=m2=20,
∴m=2$\sqrt{5}$,
即BD=2$\sqrt{5}$,AC=4$\sqrt{5}$.
∵四边形ABCD为菱形,
∴OB=$\frac{1}{2}$BD=$\sqrt{5}$,OA=$\frac{1}{2}$AC=2$\sqrt{5}$,
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=5.
∵四边形EFGH为矩形,
∴∠G=∠AOB=90°,
∴△AOB∽△AGC,
∴$\frac{OB}{CG}=\frac{OA}{AG}=\frac{AB}{AC}$,
∴CG=4,AG=8.
∴矩形EFGH的长为8,宽为4.
点评 本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质,解题的关键:(1)找出AF∥CH、DH∥BF;(2)找出关于m的一元二次方程.本题属于中档题,难度不大,但解题过程叫繁琐,解决该题型题目时,根据相似三角形的性质找出对应边的比例关系是关键.

| A. | (-1)0=0 | B. | $\sqrt{1}$=±1 | C. | $\root{3}{-1}$=1 | D. | 3-1=$\frac{1}{3}$ |
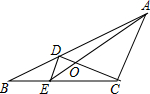 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
| A. | 长方体的截面一定是长方形 | |
| B. | 了解一批日光灯的使用寿命适合采用的调查方式是普查 | |
| C. | 一个圆形和它平移后所得的圆形全等 | |
| D. | 多边形的外角和不一定都等于360° |
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 两边及其一角相等的两个三角形全等 | |
| C. | 16的平方根是4 | |
| D. | 一组数据2,0,1,6,6的中位数和众数分别是2和6 |
 如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是(3,0).
如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是(3,0).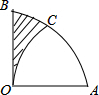 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$. 昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.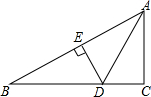 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )