题目内容
3.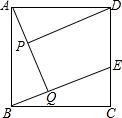 已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
分析 (1)根据正方形的性质得出AD=BA,∠BAQ=∠ADP,再根据已知条件得到∠AQB=∠DPA,判定△AQB≌△DPA并得出结论;(2)根据AQ-AP=PQ和全等三角形的对应边相等进行判断分析.
解答  解:(1)∵正方形ABCD
解:(1)∵正方形ABCD
∴AD=BA,∠BAD=90°,即∠BAQ+∠DAP=90°
∵DP⊥AQ
∴∠ADP+∠DAP=90°
∴∠BAQ=∠ADP
∵AQ⊥BE于点Q,DP⊥AQ于点P
∴∠AQB=∠DPA=90°
∴△AQB≌△DPA(AAS)
∴AP=BQ
(2)①AQ-AP=PQ
②AQ-BQ=PQ
③DP-AP=PQ
④DP-BQ=PQ
点评 本题主要考查了正方形以及全等三角形,解决问题的关键是掌握:正方形的四条边相等,四个角都是直角.解题时需要运用:有两角和其中一角的对边对应相等的两个三角形全等,以及全等三角形的对应边相等.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
13.计算(-6)÷2的结果等于( )
| A. | -4 | B. | -3 | C. | 3 | D. | -12 |
14.下列计算中正确的是( )
| A. | 2a•3a=6a | B. | (a2)3=a5 | C. | (a+3)2=a2+9 | D. | (-3a)-2=$\frac{1}{9{a}^{2}}$ |
11.下列说法正确的是( )
| A. | 长方体的截面一定是长方形 | |
| B. | 了解一批日光灯的使用寿命适合采用的调查方式是普查 | |
| C. | 一个圆形和它平移后所得的圆形全等 | |
| D. | 多边形的外角和不一定都等于360° |
8.下列命题正确的是( )
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 两边及其一角相等的两个三角形全等 | |
| C. | 16的平方根是4 | |
| D. | 一组数据2,0,1,6,6的中位数和众数分别是2和6 |
15. 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 12cm | B. | 6cm | C. | 3$\sqrt{2}$cm | D. | 2$\sqrt{3}$cm |
 如图,过反比例函数y=$\frac{k}{x}$(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
如图,过反比例函数y=$\frac{k}{x}$(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )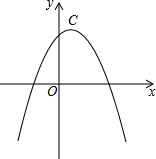 若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=-2x2+4x+2与C2:y2=-x2+mx+n为“友好抛物线”.
若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=-2x2+4x+2与C2:y2=-x2+mx+n为“友好抛物线”.