题目内容
13.某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.(1)写出月销售利润y(单位:元) 与售价x(单位:元/千克)之间的函数解析式.
(2)当售价定为多少时会获得最大利润?求出最大利润.
(3)商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
分析 (1)根据题意可以得到月销售利润y(单位:元) 与售价x(单位:元/千克)之间的函数解析式;
(2)根据(1)中的关系式化为顶点式即可解答本题;
(3)根据题意可以得到方程和相应的不等式,从而可以解答本题.
解答 解:(1)由题意可得,
y=(x-40)[500-(x-50)×10]=-10x2+1400x-40000,
即月销售利润y(单位:元) 与售价x(单位:元/千克)之间的函数解析式是y=-10x2+1400x-40000;
(2)∵y=-10x2+1400x-40000=-10(x-70)2+9000,
∴当x=70时,y取得最大值,此时y=9000,
答:当售价定为70元时会获得最大利润,最大利润是9000元;
(3)设销售单价为a元,
$\left\{\begin{array}{l}{-10{a}^{2}+1400a-40000=8000}\\{40[500-(a-50)×10]≤10000}\end{array}\right.$,
解得,a=80,
答:商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为80元.
点评 本题考查二次函数的应用、一元二次方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用二次函数的性质和方程的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
| A. | AD=BC | B. | AC=BD | C. | BC∥AD | D. | ∠A=∠B |
 如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)
如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)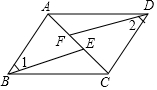 如图,在?ABCD中,点E,F为对角线AC上的两点,AF=CE.求证:∠1=∠2.
如图,在?ABCD中,点E,F为对角线AC上的两点,AF=CE.求证:∠1=∠2.