题目内容
2．
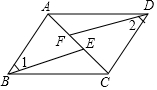如图，在?ABCD中，点E，F为对角线AC上的两点，AF=CE．求证：∠1=∠2．
分析 利用平行四边形的性质，结合已知条件可证明△ABE≌△CDF，则可证得结论．
解答 证明：
∵四边形ABCD为平行四边形，
∴AB=CD，AB∥CD，
∴∠BAE=∠DCF，
∵AF=CE，
∴AF+EF=EF+CE，即AE=CF，
在△ABE和△CDF中
$\left\{\begin{array}{l}{AB=CD}\\{∠BAE=∠DCF}\\{AE=CF}\end{array}\right.$
∴△ABE≌△CDF（SAS），
∴∠1=∠2．
点评 本题主要考查平行四边形的性质，掌握平行四边形的对边平行且相等是解题的关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
10．某旅行社暑假期间面向学生推出“上海一日游”活动，甲、乙两所学校参加该活动，收费标准如下：
已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费20800元，若两校联合组团只需花费18000元．
（1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？
（2）两所学校报名参加旅游的学生各有多少人？
（3）现从甲校抽调a人，从乙校抽调b人，去参加体验活动．甲校每位成员必须参加5个项目，乙校每位成员必须参加6个项目，他们一共参加了420次项目体验活动，是否存在一个正整数n，使得a是b的正整数倍？若存在，请求出这个n，若不存在，请说明理由．
| 人数m | 0＜m≤100 | 100＜m≤200 | m＞200 |
| 收费标准（元/人） | 90 | 85 | 75 |
（1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？
（2）两所学校报名参加旅游的学生各有多少人？
（3）现从甲校抽调a人，从乙校抽调b人，去参加体验活动．甲校每位成员必须参加5个项目，乙校每位成员必须参加6个项目，他们一共参加了420次项目体验活动，是否存在一个正整数n，使得a是b的正整数倍？若存在，请求出这个n，若不存在，请说明理由．
如图，在△ABC中，若DE∥BC，$\frac{AD}{DB}$=$\frac{2}{3}$，DE=4cm，则BC的长是10．