题目内容
7. 如图,矩形ABCD中,AB=8,BC=10,AF平分∠DAE,EF⊥AE,则CF等于3.
如图,矩形ABCD中,AB=8,BC=10,AF平分∠DAE,EF⊥AE,则CF等于3.
分析 根据矩形的对边相等可得AD=BC,角平分线的定义可得∠DAF=∠EAF,然后利用“角角边”证明△ADF和△AEF全等,根据全等三角形对应边相等可得AD=AE,EF=DF,利用勾股定理列式求出BE,再求出CE,设CF=x,表示出EF,然后利用勾股定理列方程求解即可.
解答 解:矩形ABCD中,AD=BC=10,∠D=90°,
∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵EF⊥AE,
∴∠AEF=90°,
∴∠AEF=∠D,
在△ADF和△AEF中,$\left\{\begin{array}{l}{∠DAF=∠EAF}\\{∠AEF=∠D}\\{AF=AF}\end{array}\right.$,
∴△ADF≌△AEF(AAS),
∴AD=AE=10,EF=DF,
在Rt△ABE中,根据勾股定理得,BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴CE=BC-BE=10-6=4,
设CF=x,则EF=DF=CD-CF=8-x,
在Rt△CEF中,根据勾股定理得,CE2+CF2=EF2,
即42+x2=(8-x)2,
解得x=3,
即CF=3.
故答案为:3.
点评 本题考查了矩形的性质,勾股定理,全等三角形的判定与性质,此类题目,利用勾股定理列出方程是解题的关键,也是难点.

练习册系列答案
相关题目
16.某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
| A 组 | -1.5 | +1.5 | -1 | -2 | -2 |
| B组 | +1 | +3 | -3 | +2 | -3 |
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
 已知,如图,在?ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=2cm.
已知,如图,在?ABCD中,AB=5cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=2cm.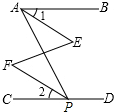 如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.
如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.