题目内容
19．实数m、n满足|m-2|+（n-2017）2=0，则m-1+n0=$\frac{3}{2}$．分析 根据非负数的和为零，可得 m，n的值，根据零次幂、负整数指数幂与正整数指数幂互为倒数，可得答案．
解答 解：由题意，得
m-2=0，n-2017=0，
解得m=2，n=2017．
m-1+n0=1+$\frac{1}{2}$=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题考查了负整数指数幂，利用非负数的和为零得出 m，n的值是解题关键．
练习册系列答案
相关题目
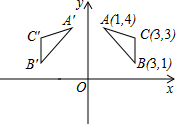如图，△A′B′C′与△ABC关于y轴对称，已知A（1，4），B（3，1），C（3，3），若以原点O为位似中心，相似比为$\frac{1}{2}$作△A′B′C′的缩小的位似图形△A″B″C″，则A″的坐标是（-$\frac{1}{2}$，2）或（$\frac{1}{2}$，-2）．
如图，矩形ABCD中，AB=8，BC=10，AF平分∠DAE，EF⊥AE，则CF等于3．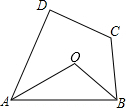
如图，在四边形ABCD中，AO平分∠DAB，BO平分∠ABC，且∠D+∠C=220°．求∠AOB的度数．