题目内容
17.观察下列各题:1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
…
(1)根据上面各式的规律,请直接写出1+3+5+7+9+…+99=2500=502;
(2)请写出第n个式子的表达式(n+1)2.
分析 (1)由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出连续奇数的和等于数的个数的平方;由此可以写出1+3+5+7+9+…+99;
(2)自然数n(n≥1)表示奇数为2n+1,因此得到一般规律.
解答 解:(1)1+3+5+7+9+…+99=2500=502;
(2)1+3+5+7+9+…+2n+1=(n+1)2;
故答案为:2500=502;(n+1)2.
点评 此题主要考查了数字的变化规律,探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法.

练习册系列答案
相关题目
 如图,矩形ABCD中,AB=8,BC=10,AF平分∠DAE,EF⊥AE,则CF等于3.
如图,矩形ABCD中,AB=8,BC=10,AF平分∠DAE,EF⊥AE,则CF等于3.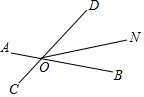 如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠DON为35度.
如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠DON为35度.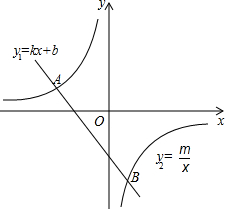 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-3,1)、B(1.5,n)两点.若y1>y2,则x的取值范围是x<-3或0<x<1.5.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-3,1)、B(1.5,n)两点.若y1>y2,则x的取值范围是x<-3或0<x<1.5.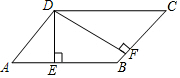 如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为( )cm.
如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为( )cm.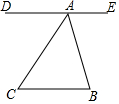 如图所示,已知DE∥BC,AC平分∠BAD,∠B=80°,求∠C的大小.
如图所示,已知DE∥BC,AC平分∠BAD,∠B=80°,求∠C的大小.